affineplane

Affineplane API Documentation v2.19.0

Welcome to affineplane API reference documentation. These docs are generated with yamdog.

See also Usage and GitHub for introduction and source code.

affineplane

The affineplane module provides functions for affine 2D and 3D geometry. The functions are grouped in the following submodules.

Contents:

• affineplane.angle
• affineplane.box2
• affineplane.box3
• affineplane.circle2
• affineplane.circle3
• affineplane.dir2
• affineplane.dir3
• affineplane.dist2
• affineplane.dist3
• affineplane.epsilon
• affineplane.helm2
• affineplane.helm3
• affineplane.line2
• affineplane.line3
• affineplane.orient2
• affineplane.path2
• affineplane.path3
• affineplane.plane2
• affineplane.plane3
• affineplane.point2
• affineplane.point3
• affineplane.poly2
• affineplane.quat4
• affineplane.ray3
• affineplane.rect2
• affineplane.rect3
• affineplane.rot2
• affineplane.scalar1
• affineplane.scalar2
• affineplane.scalar3
• affineplane.segment2
• affineplane.segment3
• affineplane.size2
• affineplane.size3
• affineplane.sphere2
• affineplane.sphere3
• affineplane.vec2
• affineplane.vec3
• affineplane.vec4
• affineplane.version

Source: lib/index.js

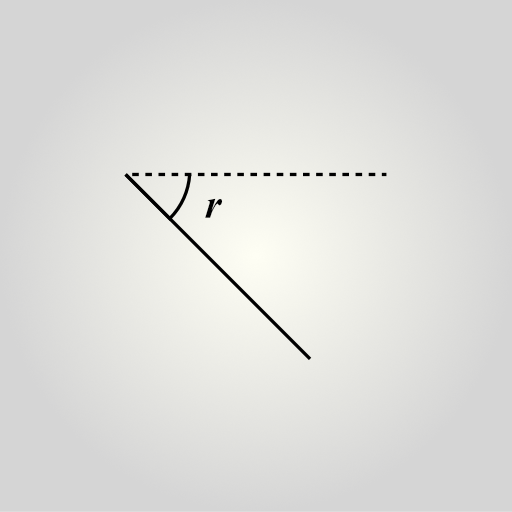
affineplane.angle

Common utilites to handle angles.

Contents:

• affineplane.angle.degToRad
• affineplane.angle.modulo
• affineplane.angle.radToDeg

Source: angle/index.js

affineplane.angle.degToRad(deg)

Convert angle from degrees to radians, for example 720 becomes 4π.

Parameters:

• deg
  • a number, an angle in degrees.

Returns:

• a number, the angle in radians.

Source: degToRad.js

affineplane.angle.modulo(r)

Limit an angle between ]-PI, +PI] but preserve the direction. This can be used to preprocess user input, for example to normalize 4*PI as 0.

Parameters:

• r
  • angle in radians, allowed to be outside ]-PI, +PI].

Returns:

• a number, the angle in radians and between ]-PI, +PI]

Source: modulo.js

affineplane.angle.radToDeg(rad)

Convert angle from radians to degrees. For example 4π becomes 720.

Parameters:

• rad
  • a number, an angle in radians.

Returns:

• a number, the angle in degrees.

Source: radToDeg.js

affineplane.box2

Two-dimensional rectangle. Unlike size2, box2 has location and orientation and thus can be represented in any basis without loss of information.

Represented with an object { a, b, x, y, w, h } where

• a,b provide orientation with respect to the reference basis. The norm of vector (a,b) is always 1.
• x,y provide origin position in the reference basis.
• w,h provide box size on the reference basis.

Contents:

• affineplane.box2.UNIT
• affineplane.box2.ZERO
• affineplane.box2.almostEqual
• affineplane.box2.at
• affineplane.box2.atBox
• affineplane.box2.atNorm
• affineplane.box2.collide
• affineplane.box2.create
• affineplane.box2.fromPoints
• affineplane.box2.getAngle
• affineplane.box2.getArea
• affineplane.box2.getBasis
• affineplane.box2.getBasisInverse
• affineplane.box2.getBounds
• affineplane.box2.getCircle
• affineplane.box2.getInnerSquare
• affineplane.box2.getMinimumBounds
• affineplane.box2.getPath
• affineplane.box2.getPoints
• affineplane.box2.getPolygon
• affineplane.box2.getSegments
• affineplane.box2.getSize
• affineplane.box2.getSphere
• affineplane.box2.hasPoint
• affineplane.box2.homothety
• affineplane.box2.offset
• affineplane.box2.projectTo
• affineplane.box2.projectToPlane
• affineplane.box2.resizeBy
• affineplane.box2.resizeTo
• affineplane.box2.rotateBy
• affineplane.box2.scaleBy
• affineplane.box2.transitFrom
• affineplane.box2.transitTo
• affineplane.box2.translate
• affineplane.box2.validate

Source: box2/index.js

affineplane.box2.UNIT

An origin-centered box with unit width and height.

Source: box2/index.js

affineplane.box2.ZERO

A zero-size box.

Source: box2/index.js

affineplane.box3.UNIT

An origin-centered box with unit width, height, and depth.

Source: box3/index.js

affineplane.box3.ZERO

A zero-size box.

Source: box3/index.js

affineplane.box2.almostEqual(b, bb[, tolerance])

Are two boxes almost equal?

Parameters:

• b
  • a box2
• bb
  • a box2
• tolerance
  • optional number, default is affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.box2.at(box, rx, ry)

Take a point on the box, represented in the reference basis.

Parameters:

• box
  • a box2
• rx
  • horizontal distance from the top-left corner of the box represented on the box’s inner basis. The unit of distance is same in the reference basis.
• ry
  • vertical distance from the top-left corner of the box represented on the box’s inner basis. The unit of distance is same in the reference basis.

Returns:

• a point2 in the reference basis.

Source: at.js

affineplane.box2.atBox(box, x, y)

Take a point in the reference basis and represent it in the box basis. This is like affineplane.box2.at but to the other direction.

Parameters:

• box
  • a box2
• x
  • horizontal coordinate in the reference basis.
• y
  • vertical coordinate in the reference basis.

Returns:

• a point2 in the box basis.

Source: atBox.js

affineplane.box2.atNorm(box, nw, nh)

Take a point on the box at the normalized coordinates.

Parameters:

• box
  • a box2
• nw
  • a number, a normalized coordinate along width 0..1
• nh
  • a number, a normalized coordinate along height 0..1

Returns:

• a point2 in the reference basis.

Source: atNorm.js

affineplane.box2.collide(b, bb)

Do two boxes collide?

Parameters:

• b
  • a box2, in the reference basis
• bb
  • a box2, in the reference basis

Returns:

• a boolean, true if boxes collide.

Source: collide.js

affineplane.box2.create(plane, size)

Create a box2 object.

Parameters:

• plane
  • a plane2 on the reference basis. Defines the box origin and orientation. Scale is defaulted to 1.
• size
  • a size2 on the reference basis. Defines the box size.

Returns:

• a box2

Source: create.js

affineplane.box2.fromPoints(points)

Get a rectangular boundary of the given points. In other words, compute such a box that has no rotation and no dilation with respect to the reference basis but has translation and size so that it covers the given points.

Parameters:

• points
  • array of point2, each in the reference basis.

Returns:

• a box2, in the reference basis.

Source: fromPoints.js

affineplane.box2.getAngle(box)

Compute box angle in radians with respect to the reference basis.

Parameters:

• box
  • a box2, in the reference basis.

Returns:

• a number, the angle in radians.

Source: getAngle.js

affineplane.box2.getArea(box)

Compute box area. This returns the area in the reference basis.

Parameters:

• box
  • a box2, in the reference basis.

Returns:

• a number, the area in the reference basis.

Source: getArea.js

affineplane.box2.getBasis(box)

Get the inner basis of the box. In other words, represent the box inner basis as a plane in the reference basis. The scale of the resulting basis is always 1. See also affineplane.box2.getBasisInverse.

Parameters:

• box
  • a box2 in the reference basis.

Returns:

• a plane2 in the reference basis.

Source: getBasis.js

affineplane.box2.getBasisInverse(box)

Get the outer basis of the box represented in the box basis. The scale of the resulting basis is always 1. See also affineplane.box2.getBasis.

Parameters:

• box
  • a box2 in the reference basis.

Returns:

• a plane2 in the box basis. The outer basis.

Source: getBasisInverse.js

affineplane.box2.getBounds(boxes)

Get outer rectangular boundary of the given box or boxes. In other words, compute such a box that has no rotation and no dilation with respect to the reference basis but has translation and size so that it covers the given box or boxes.

Parameters:

• boxes
  • a box2, in the reference basis.
  • array of box2, each in the reference basis.

Returns:

• a box2, in the reference basis.

Source: getBounds.js

affineplane.box2.getCircle(box)

Get the circumscribed circle of the box. In other words, get the circle that contains the box so that the box corners are on it. The resulting circle is also the minimum bounding circle of the box.

Parameters:

• box
  • a box2, in the reference basis.

Returns:

• a sphere2

Aliases: affineplane.box2.getSphere

Source: getCircle.js

affineplane.box2.getInnerSquare(box)

Get the largest square that fits inside the box and has the same center.

Parameters:

• box
  • a box2, in the reference basis.

Returns:

• a box2, in the reference basis.

Source: getInnerSquare.js

affineplane.box2.getMinimumBounds(boxes)

Find approximate minimum bounding box aka minimum area rectangle (MAR). Such MAR contains all the given set of boxes. The orientation of the resulting bounding box is not necessarily parallel with the reference basis.

Parameters:

• boxes
  • array of box2

Returns:

• a box2

Source: getMinimumBounds.js

affineplane.box2.getPath(box)

Get the box corner points as a path. Points are in clock-wise order.

Parameters:

• box

Returns:

• a path2

Aliases: affineplane.box2.getPoints, affineplane.box2.getPolygon

Source: getPath.js

affineplane.box2.getPoints

Alias of affineplane.box2.getPath

affineplane.box2.getPolygon

Alias of affineplane.box2.getPath

affineplane.box2.getSegments(box)

Get the four line segments of the box.

Parameters:

• box
  • a box2, in the reference basis.

Returns:

• array of segment2, each segment in the reference basis.

Source: getSegments.js

affineplane.box2.getSize(box)

Get the size of the box.

Parameters:

• box
  • a box2 in the reference basis.

Returns:

• a size2 in the reference basis.

Source: getSize.js

affineplane.box2.getSphere

Alias of affineplane.box2.getCircle

affineplane.box2.hasPoint(box, point)

Test if a point is inside the box. If the point is at the box edge, it is counted as being inside.

Parameters:

• box
  • a box2, in the reference basis.
• point
  • a point2, in the reference basis.

Returns:

• a boolean

Source: hasPoint.js

affineplane.box2.homothety(box, origin, ratio)

Perform homothety about the origin. In other words, scale the box about the fixed pivot point.

Parameters:

• box
  • a box2, the box to be scaled.
• origin
  • a point2, the fixed origin point.
• ratio
  • a number, the scaling ratio.

Returns:

• a box2

Aliases: affineplane.box2.scaleBy

Source: homothety.js

affineplane.box2.offset(box, dx, dy)

Move the box horizontally and vertically.

Parameters:

• box
  • a box2
• dx
  • a number
• dy
  • a number

Returns:

• a box2

Source: offset.js

affineplane.box2.projectTo

Alias of affineplane.box2.projectToPlane

affineplane.box2.projectToPlane(box, target[, camera])

Project a box onto a target plane in 3d. If a camera is given, project perspectively. Otherwise, project orthogonally.

Parameters:

• box
  • a box2 in the reference basis, assume z=0.
• target
  • a plane3 in the reference basis.
• camera
  • optional point3 in the reference basis.

Returns:

• a box2 on the target plane.

Aliases: affineplane.box2.projectTo

Source: projectToPlane.js

affineplane.box2.resizeBy(box, origin, dw, dh)

Resize the box with respect to a fixed origin by the specified amounts. For example, this allows resizing the box by its center point. The operation does not change the box orientation.

Parameters:

• box
  • a box2, in the reference basis
• origin
  • a point2, in the reference basis. The origin is allowed to be outside the box but will be capped to the nearest point within the box.
• dw
  • a number, the width increase. Can be negative.
• dh
  • a number, the height increase. Can be negative.

Returns:

• a box2

Source: resizeBy.js

affineplane.box2.resizeTo(box, origin, width, height)

Resize the box to the given width and height. The origin point stays fixed relative to the box size. For example, this allows resizing the box by its center point. The operation does not change the box orientation.

Parameters:

• box
  • a box2, in the reference basis
• origin
  • a point2, in the reference basis. The origin is allowed to be outside the box but will be capped to the nearest point within the box.
• width
  • a positive number, the new width.
• height
  • a positive number, the new height.

Returns:

• a box2

Source: resizeTo.js

affineplane.box2.rotateBy(box, origin, radians)

Rotate the box around an origin point by an angle in radians. Rotation direction is from positive x axis towards positive y axis.

Parameters:

• box
  • a box2, in the reference basis
• origin
  • a point2 in the reference basis.
• radians
  • a number, rotation angle in radians.

Returns:

• a box2

Source: rotateBy.js

affineplane.box2.scaleBy(box, origin, ratio)

Alias of affineplane.box2.homothety

affineplane.box2.transitFrom(box, source)

Convert a box from source basis to the reference basis.

Parameters:

• box
  • a box2, a box in the source basis.
• source
  • a plane2, the source basis represented in the reference basis.

Returns:

• a box2, represented in the reference basis.

Source: transitFrom.js

affineplane.box2.transitTo(box, target)

Convert a box from the reference basis to the target basis.

Parameters:

• box
  • a box2, a rectangle in the reference basis.
• target
  • a plane2, the target basis represented in the reference basis.

Returns:

• a box2, represented in the target basis.

Source: transitTo.js

affineplane.box2.translate(box, vec)

Move the box horizontally and vertically by a vector. See affineplane.box2.offset to move by scalars.

Parameters:

• box
  • a box2
• vec
  • a vec2

Returns:

• a box2

Source: translate.js

affineplane.box2.validate(b)

Check if the object is a valid box2. Valid box2 has properties a and b that represent valid rotation matrix, properties x and y that are valid numbers, and properties w and h that represent size.

Parameters:

• b
  • an object

Returns:

• a boolean, true if valid box2

Source: validate.js

affineplane.box3

Three-dimensional cuboid that has the front face parallel with xy-plane. Unlike size3, box3 has location and orientation and thus can be represented in any basis without loss of information.

Represented with an object { a, b, x, y, z, w, h, d } where

• a,b provide orientation on xy-plane with respect to the reference basis.
• x,y,z provide origin position in the reference basis.
• w,h,d provide box size on the reference basis.

Contents:

• affineplane.box3.UNIT
• affineplane.box3.ZERO
• affineplane.box3.almostEqual
• affineplane.box3.at
• affineplane.box3.atBox
• affineplane.box3.atNorm
• affineplane.box3.collide
• affineplane.box3.create
• affineplane.box3.fromPoints
• affineplane.box3.getAngle
• affineplane.box3.getBasis
• affineplane.box3.getBasisInverse
• affineplane.box3.getBounds
• affineplane.box3.getMinimumBounds
• affineplane.box3.getSize
• affineplane.box3.getSphere
• affineplane.box3.getVolume
• affineplane.box3.hasPoint
• affineplane.box3.homothety
• affineplane.box3.projectTo
• affineplane.box3.projectToPlane
• affineplane.box3.resizeBy
• affineplane.box3.resizeTo
• affineplane.box3.rotateBy
• affineplane.box3.scaleBy
• affineplane.box3.transitFrom
• affineplane.box3.transitTo
• affineplane.box3.translate
• affineplane.box3.translateBy
• affineplane.box3.validate

Source: box3/index.js

affineplane.box3.almostEqual(b, bb[, tolerance])

Are two boxes almost equal?

Parameters:

• b
  • a box3
• bb
  • a box3
• tolerance
  • optional number, default is affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.box3.at(box, rx, ry, rz)

Take a point on the box, represented in the reference basis.

Parameters:

• box
  • a box3
• rx
  • horizontal distance from the left side of the box represented on the box’s inner basis. The unit of distance is same in the reference basis because the box has fixed scale of 1.
• ry
  • vertical distance from the top side of the box represented on the box’s inner basis. The unit of distance is same in the reference basis.
• rz
  • distal distance from the front side of the box represented on the box’s inner basis. The unit of distance is same in the reference basis.

Returns:

• a point3 in the reference basis.

Source: at.js

affineplane.box3.atBox(box, x, y, z)

Take a point in the reference basis and represent it in the box basis. This is like affineplane.box3.at but to the other direction.

Parameters:

• box
  • a box3
• x
  • horizontal coordinate in the reference basis.
• y
  • vertical coordinate in the reference basis.
• z
  • depth coordinate in the reference basis.

Returns:

• a point3 in the box basis.

Source: atBox.js

affineplane.box3.atNorm(box, nw, nh, nd)

Take a point on the box with coordinates normalized to box sizes.

Parameters:

• box
  • a box3
• nw
  • a number, a normalized coordinate 0..1 along width
• nh
  • a number, a normalized coordinate 0..1 along height
• nd
  • a number, a normalized coordinate 0..1 along depth

Returns:

• a point3 in the reference basis.

Source: atNorm.js

affineplane.box3.collide(b, bb)

Test if the two boxes collide. The boxes collide when the intersection of their solid cuboids is not empty.

Parameters:

• b
  • a box3, in the reference basis
• bb
  • a box3, in the reference basis

Returns:

• a boolean, true if boxes collide.

Source: collide.js

affineplane.box3.create(basis, size)

Create a box3 object.

Parameters:

• basis
  • a plane3 on the reference basis. Defines the box origin and orientation.
• size
  • a size3 on the reference basis. Defines the box size.

Returns:

• a box3

Source: create.js

affineplane.box3.fromPoints(points)

Get a cuboid boundary of the given points. In other words, compute such a 3D box that has no rotation and no dilation with respect to the reference basis but has translation and size so that it encloses the given points.

Parameters:

• points
  • array of point3, each in the reference basis.

Returns:

• a box3, in the reference basis.

Source: fromPoints.js

affineplane.box3.getAngle(box)

Compute box angle in radians with respect to the reference basis.

Parameters:

• box
  • a box2, in the reference basis.

Returns:

• a number, the angle in radians.

Source: getAngle.js

affineplane.box3.getBasis(box)

Get the inner basis of the box. The scale of the resulting basis is always 1.

Parameters:

• box
  • a box3 in the reference basis.

Returns:

• a plane3 in the reference basis.

Source: getBasis.js

affineplane.box3.getBasisInverse(box)

Get the outer basis of the box represented in the box basis. The scale of the resulting basis is always 1. See also affineplane.box3.getBasis.

Parameters:

• box
  • a box3 in the reference basis.

Returns:

• a plane3 in the box basis. The outer basis.

Source: getBasisInverse.js

affineplane.box3.getBounds(boxes)

Get outer cuboid boundary of the given box or boxes. In other words, compute such a box that has no rotation and no dilation with respect to the reference basis but has translation and size so that it covers all the given boxes.

Parameters:

• boxes
  • a box3, in the reference basis.
  • array of box3, each in the reference basis.

Returns:

• a box3, in the reference basis.

Source: getBounds.js

affineplane.box3.getMinimumBounds(boxes)

Find approximate minimum bounding box. Such a box contains all the given set of boxes. The orientation of the resulting bounding box (on xy-plane) is selected so that the box volume is minimal. Thus the orientation is not necessarily parallel with the reference basis.

Parameters:

• boxes
  • array of box3

Returns:

• a box3

Source: getMinimumBounds.js

affineplane.box3.getSize(box)

Get the size of the box.

Parameters:

• box
  • a box3 in the reference basis.

Returns:

• a size3 in the reference basis.

Source: getSize.js

affineplane.box3.getSphere(box)

Get the circumscribed sphere of the box. In other words, get the sphere that contains the box so that the box corners are on the sphere. The resulting sphere is also the minimum bounding sphere of the box.

Parameters:

• box
  • a box3, in the reference basis.

Returns:

• a sphere3

Source: getSphere.js

affineplane.box3.getVolume(box)

Compute box volume. This returns the volume as a measure in the reference basis.

Parameters:

• box
  • a box3, a cuboid in the reference basis.

Returns:

• a number, the volume in the reference basis.

Source: getVolume.js

affineplane.box3.hasPoint(box, point)

Test if a point is inside the box. If the point is at the box edge, it is counted as being inside.

Parameters:

• box
  • a box3, in the reference basis.
• point
  • a point3, in the reference basis.

Returns:

• a boolean

Source: hasPoint.js

affineplane.box3.homothety(box, origin, ratio)

Perform homothety about an origin point. In other words, scale the box about the fixed pivot point.

Parameters:

• box
  • a box3, the box to be scaled.
• origin
  • a point3, the fixed pivot point.
• ratio
  • a number, the scaling ratio.

Returns:

• a box3

Aliases: affineplane.box3.scaleBy

Source: homothety.js

affineplane.box3.projectTo

Alias of affineplane.box3.projectToPlane

affineplane.box3.projectToPlane(box, target[, camera])

Project a 3D box onto a target plane. If a camera is given, project perspectively. Otherwise, project orthogonally along z axis. The resulting box is in 2D.

We only project the front face of the 3D box. This is because if we projected a full 3D box perspectively, we would get a lattice mesh in which we are not currently interested. To scale the box towards camera, see affineplane.box3.homothety.

Parameters:

• box
  • a box3 in the reference basis.
• target
  • a plane3 in the reference basis.
• camera
  • optional point3 in the reference space. The camera position.

Returns:

• a box2 on the target plane.

Aliases: affineplane.box3.projectTo

Source: projectToPlane.js

affineplane.box3.resizeBy(box, origin, dw, dh, dd)

Resize the box with respect to a fixed origin by the specified amounts. For example, this allows resizing the box by its center point. The operation does not change the box orientation.

Parameters:

• box
  • a box3, in the reference basis
• origin
  • a point3, in the reference basis. The origin is allowed to be outside the box but will be capped to the nearest point within the box.
• dw
  • a number, the width increase. Can be negative.
• dh
  • a number, the height increase. Can be negative.
• dd
  • a number, the depth increase. Can be negative.

Returns:

• a box3

Source: resizeBy.js

affineplane.box3.resizeTo(box, origin, width, height, depth)

Resize the box to the given width, height, and depth. The origin point stays fixed relative to the box size. For example, this allows resizing the box by its center point. The operation does not change the box orientation.

Parameters:

• box
  • a box3, in the reference basis
• origin
  • a point3, in the reference basis. The origin is allowed to be outside the box but will be capped to the nearest point within the box.
• width
  • a positive number, the new width.
• height
  • a positive number, the new height.
• depth
  • a positive number, the new depth.

Returns:

• a box3

Source: resizeTo.js

affineplane.box3.rotateBy(box, origin, radians)

Rotate the box around an origin point by an angle in radians. Rotation direction is from positive x axis towards positive y axis.

Parameters:

• box
  • a box3, in the reference basis
• origin
  • a point3 in the reference basis.
• radians
  • a number, rotation angle in radians.

Returns:

• a box3

Source: rotateBy.js

affineplane.box3.scaleBy(box, origin, ratio)

Alias of affineplane.box3.homothety

affineplane.box3.transitFrom(box, source)

Convert a box from source basis to the reference basis.

Parameters:

• box
  • a box3, a cuboid in the source basis.
• source
  • a plane3, the source basis represented in the reference basis.

Returns:

• a box3, represented in the reference basis.

Source: transitFrom.js

affineplane.box3.transitTo(box, target)

Convert a box from the reference basis to the target basis.

Parameters:

• box
  • a box3, a cuboid in the reference basis.
• target
  • a plane3, the target basis represented in the reference basis.

Returns:

• a box3, represented in the target basis.

Source: transitTo.js

affineplane.box3.translate(box, vec)

Move the box by the given vector. See affineplane.box3.offset to translate by scalars.

Parameters:

• box
  • a box3
• vec
  • a vec3 or vec2

Returns:

• a box3

Source: translate.js

affineplane.box3.translateBy(box, dx, dy, dz)

Move the box along x, y, and/or z axis by the given amounts.

Parameters:

• box
  • a box3
• dx
  • a number
• dy
  • a number
• dz
  • a number

Returns:

• a box3

Source: offset.js

affineplane.box3.validate(b)

Check if the object is a valid box3. Valid box3 has properties a and b that represent valid rotation matrix, properties x, y, z that are valid numbers, and properties w, h, d that represent size.

Parameters:

• b
  • an object

Returns:

• a boolean, true if valid box2

Source: validate.js

affineplane.circle2

Alias of affineplane.sphere2

affineplane.circle3

Flat round circle in three dimensional space. Parallel to the xy-plane.

Represented with an object { x, y, z, r } for the origin and the radius.

Contents:

• affineplane.circle3.UNIT
• affineplane.circle3.ZERO
• affineplane.circle3.almostEqual
• affineplane.circle3.area
• affineplane.circle3.atCenter
• affineplane.circle3.boundingBox
• affineplane.circle3.boundingCircle
• affineplane.circle3.collide
• affineplane.circle3.collideCircle
• affineplane.circle3.collideSegment
• affineplane.circle3.copy
• affineplane.circle3.create
• affineplane.circle3.hasPoint
• affineplane.circle3.homothety
• affineplane.circle3.offset
• affineplane.circle3.polarOffset
• affineplane.circle3.projectTo
• affineplane.circle3.projectToPlane
• affineplane.circle3.rotateBy
• affineplane.circle3.scaleBy
• affineplane.circle3.size
• affineplane.circle3.transitFrom
• affineplane.circle3.transitTo
• affineplane.circle3.translate
• affineplane.circle3.validate

Source: circle3/index.js

affineplane.circle3.UNIT

The unit circle, radius=1.

Source: circle3/index.js

affineplane.circle3.ZERO

A zero-radius circle.

Source: circle3/index.js

affineplane.circle3.almostEqual(c, d[, tolerance])

Test if two circles are almost equal by the margin of tolerance.

Parameters:

• c
  • a circle3
• d
  • a circle3
• tolerance
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.circle3.area(c)

Get area of the circle.

Parameters:

• a circle3

Returns:

• a scalar2, a number representing area

Source: area.js

affineplane.circle3.atCenter(c)

Get the center point of the circle. Note that the circle3 object itself can act as a point3 in many cases.

Parameters:

• c
  • a circle3

Returns:

• a point3

Source: atCenter.js

affineplane.circle3.boundingBox(circle)

Get outer cuboid boundary of the given circle.

Parameters:

• circle
  • a circle3, in the reference basis.

Returns:

• a box3, in the reference basis.

Source: boundingBox.js

affineplane.circle3.boundingCircle(circles)

Find a circle that encloses all the given circles when projected onto the same xy-plane. The resulting circle shares the largest z coordinate of the given circles. The result is approximate but is quaranteed to contain the optimal (projected) bounding circle.

Parameters:

• circles
  • an array of circle3

Returns:

• a circle3

Source: boundingCircle.js

affineplane.circle3.collide(c, cc)

Detect collision between two circles.

Parameters:

• c
  • a circle3
• cc
  • a circle3

Returns:

• boolean, true if the circles collide

Aliases: affineplane.circle3.collideCircle

Source: collide.js

affineplane.circle3.collideCircle(c, cc)

Alias of affineplane.circle3.collide

affineplane.circle3.collideSegment(c, seg)

Detect collision between a circle and a line segment.

Parameters:

• c
  • a circle3
• seg
  • a segment3

Returns:

• boolean, true if the shapes collide

Source: collideSegment.js

affineplane.circle3.copy(c)

Copy a circle object.

Parameters:

• c
  • a circle3

Returns:

• a circle3

Source: copy.js

affineplane.circle3.create(x, y, z, r)

Create a circle object in 3D. The circle is a flat round shape parallel to xy-plane.

Parameters:

• x
  • a number
• y
  • a number
• z
  • a number
• r
  • a number, the radius

Returns:

• a circle3

Source: create.js

affineplane.circle3.hasPoint(c, point)

Detect collision between a circle and a point.

Parameters:

• c
  • a circle3
• point
  • a point2

Returns:

• boolean, true if the point is at the edge or inside the circle.

Source: hasPoint.js

affineplane.circle3.homothety(circle, origin, ratio)

Perform homothety for the circle about a pivot. In other words, scale the circle by the given ratio, so that the origin point stays fixed.

Parameters:

• circle
  • a circle3
• origin
  • a point3, the transform origin, the pivot point
• ratio
  • a number, the scaling ratio

Returns:

• a circle3

Aliases: affineplane.circle3.scaleBy

Source: homothety.js

affineplane.circle3.offset(c, dx, dy[, dz])

Offset a circle by scalars dx, dy, dz. See affineplane.circle3.translate to offset by a vector.

Parameters:

• c
  • a circle3
• dx
  • a number, an offset along x-axis.
• dy
  • a number, an offset along y-axis.
• dz
  • optional number. The offset along z-axis, default is 0.

Returns:

• a circle3, translated

Source: offset.js

affineplane.circle3.polarOffset(circle, distance, theta[, phi])

Offset a circle by the given distance towards the direction given by the spherical theta and phi angles.

Parameters:

• circle
  • a circle3
• distance
  • a number, the distance from p.
• theta
  • a number, the angle around z-axis, the azimuthal angle. Clockwise rotation, following the right-hand rule.
• phi
  • optional number, default π/2. The polar angle in radians measured from the positive z-axis.

Returns:

• a circle3

Source: polarOffset.js

affineplane.circle3.projectTo

Alias of affineplane.circle3.projectToPlane

affineplane.circle3.projectToPlane(circle, plane[, camera])

Project a circle onto a plane in 3D space. The result is a 2D circle. If the camera is undefined, project orthogonally.

Parameters:

• sphere
  • a circle3 in the reference space.
• plane
  • a plane3 in the reference space. The target plane.
• camera
  • optional point3 in the reference space. The camera position.

Returns:

• a circle2 on the target plane.

Aliases: affineplane.circle3.projectTo

Source: projectToPlane.js

affineplane.circle3.rotateBy(c, origin, radians)

Rotate a circle about a line parallel to z-axis that goes through the given origin point. The rotation direction follows the right hand rule about the positive z-axis.

Parameters:

• c
  • a circle3
• origin
  • a point3, the point that defines the line around which to rotate
• radians
  • a number, angle in radians

Returns:

• a circle3, the rotated circle

Source: rotateBy.js

affineplane.circle3.scaleBy

Alias of affineplane.circle3.homothety

affineplane.circle3.size(c)

Get the cuboid size of a circle. Circles always have zero depth.

Parameters:

• c
  • a circle3 in the reference basis.

Returns:

• a size3 in the reference basis.

Source: size.js

affineplane.circle3.transitFrom(circle, source)

Transit a circle3 from the source basis to the reference basis.

Parameters:

• circle
  • a circle3 in the source basis.
• source
  • a plane3, the source basis, represented in the reference basis.

Returns:

• a circle3, represented in the reference basis.

Source: transitFrom.js

affineplane.circle3.transitTo(circle, target)

Transit a circle3 to the target basis from the reference basis.

Parameters:

• circle
  • a circle3 in the source basis.
• source
  • a plane3, the source basis, represented in the reference basis.

Returns:

• a circle3, represented in the reference basis.

Source: transitTo.js

affineplane.circle3.translate(c, vec)

Translate a circle by the vector. Does not affect radius. See affineplane.circle3.offset to translate by scalars.

Parameters:

• c
  • a circle3
• vec
  • a vec3

Returns:

• a circle3, translated

Source: translate.js

affineplane.circle3.validate(c)

Check if the object is a valid circle3. A valid circle3 has x, y, z, r properties that are valid numbers.

Parameters:

• c
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.dir2

A direction on 2D space, represented by the object { x, y }.

A direction is basically a unit vector. When a direction is transited between planes, only the rotation of the coordinate space affects the direction. Scale change does not affect it.

Contents:

• affineplane.dir2.copy
• affineplane.dir2.create
• affineplane.dir2.fromPolar
• affineplane.dir2.fromVector
• affineplane.dir2.projectTo
• affineplane.dir2.projectToPlane
• affineplane.dir2.toAngle
• affineplane.dir2.toPolar
• affineplane.dir2.toVector
• affineplane.dir2.transitFrom
• affineplane.dir2.transitTo
• affineplane.dir2.validate

Source: dir2/index.js

affineplane.dir2.copy(dir)

Copy direction object.

Parameters:

• dir
  • a dir2

Returns:

• a dir2

Source: copy.js

affineplane.dir2.create

Alias of affineplane.dir2.fromPolar

affineplane.dir2.fromPolar(r)

Create a new direction from an angle.

Parameters:

• r
  • a number. The angle in radians.

Returns:

• a dir2

Aliases: affineplane.dir2.create

Source: fromPolar.js

affineplane.dir2.fromVector(v)

Create a new direction from a vector. Basically, extract an unit vector from the given vector. If given a zero vector, return a direction towards positive x-axis.

Parameters:

• v
  • a vec2

Returns:

• a dir2

Source: fromVector.js

affineplane.dir2.projectTo

Alias of affineplane.dir2.projectToPlane

affineplane.dir2.projectToPlane(dir, plane)

Project a 2D direction onto a 2D plane. Perspective does not affect the direction.

Parameters:

• dir
  • a dir2 in the reference basis.
• plane
  • a plane3 in the reference basis. The image plane.

Returns:

• a dir2 on the image plane.

Aliases: affineplane.dir2.projectTo

Source: projectToPlane.js

affineplane.dir2.toAngle

Alias of affineplane.dir2.toPolar

affineplane.dir2.toPolar(dir)

Get the direction as angle around z-axis measured from positive x-axis.

Parameters:

• dir
  • a dir2 object or unit vec2.

Returns:

• a number, an angle in radians in ]-π, π].

Aliases: affineplane.dir2.toAngle

Source: toPolar.js

affineplane.dir2.toVector(dir, magn)

Get a vector from the direction with the given length.

Parameters:

• dir
  • a dir2
• magn
  • a number, the magnitude of the vector to create.

Returns:

• a vec2

Source: toVector.js

affineplane.dir2.transitFrom(dir, source)

Transit a direction from the source plane to the reference plane.

Parameters:

• dir
  • a dir2 on the source plane.
• source
  • a plane2, the source plane, represented on the reference plane.

Returns:

• a dir2, represented on the reference plane.

Source: transitFrom.js

affineplane.dir2.transitTo(dir, target)

Transit a dir2 to a target plane. In other words, represent the direction in the coordinate system of the target plane.

Parameters:

• dir
  • a number, a dir2 on the reference plane.
• target
  • a plane2, the target plane, represented on the reference plane.

Returns:

• a dir2 on the target plane.

Source: transitTo.js

affineplane.dir2.validate(d)

Check if object is a valid dir2. Valid dir2 is an object with properties x,y that represent a unit vector.

Parameters:

• d
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.dir3

A direction in 3D, represented by the object { x, y, z }.

The direction is basically a unit vector that carries semantics of direction. Under a change of the reference frame, the change in translation and scale do not affect the direction, only the change in orientation (=attitude) does.

Contents:

• affineplane.dir3.almostEqual
• affineplane.dir3.almostEqual
• affineplane.dir3.copy
• affineplane.dir3.create
• affineplane.dir3.fromSpherical
• affineplane.dir3.fromVector
• affineplane.dir3.projectTo
• affineplane.dir3.projectToPlane
• affineplane.dir3.toSpherical
• affineplane.dir3.toVector
• affineplane.dir3.transitFrom
• affineplane.dir3.transitTo
• affineplane.dir3.validate

Source: dir3/index.js

affineplane.dir3.almostEqual(d, dd[, epsilon])

Test if directions are almost equal by the margin of epsilon. The directions are compared as two unit vectors.

Parameters:

• d
  • a dir2
• dd
  • a dir2
• epsilon
  • Optional number, default to affineplane.epsilon.
  • Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.dir3.almostEqual(d, dd[, epsilon])

Test if directions are almost equal by the margin of epsilon. The directions are compared as two unit vectors.

Parameters:

• d
  • a dir3
• dd
  • a dir3
• epsilon
  • Optional number, default to affineplane.epsilon.
  • Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.dir3.copy(dir)

Copy direction object.

Parameters:

• dir
  • a dir3

Returns:

• a dir3

Source: copy.js

affineplane.dir3.create

Alias of affineplane.dir3.fromSpherical

affineplane.dir3.fromSpherical(theta, phi)

Create a direction in 3D space from two angles. The angles correspond to azimuthal and polar angles in the spherical coordinates system when z-axis is considered the polar axis.

Parameters:

• theta
  • a number, an angle in radians around z-axis from positive x-axis.
  • Gives the direction on xy-plane.
  • In geographical terms, a longitude when z-axis points the north pole.
  • In spherical coordinate system, this is often called azimuthal angle.
• phi
  • a number, an angle in radians from the positive z-axis.
  • The angle π/2 corresponds to a direction perpendicular to z-axis.
  • In geographical terms, a latitude if measured from the north pole.
  • In spherical coordinate system, this is often called polar angle.

Returns:

• a dir3

Examples:

• Toward positive x-axis: dir3.fromSpherical(0, π/2)
• Toward positive y-axis: dir3.fromSpherical(π/2, π/2)
• Toward positive z-axis: dir3.fromSpherical(0, 0)
• Toward point (1,1,1): dir3.fromSpherical(π/4, π/4)

Aliases: affineplane.dir3.create

Source: fromSpherical.js

affineplane.dir3.fromVector(vec)

Create a new direction from a vector. Basically extract an unit vector from the vector. If the case of zero vector, return the default direction towards positive x-axis.

Parameters:

• vec
  • a vec3, represented in the reference frame.

Returns:

• a dir3

Source: fromVector.js

affineplane.dir3.projectTo

Alias of affineplane.dir3.projectToPlane

affineplane.dir3.projectToPlane(dir, plane)

Project a 3D direction onto a 2D plane orthogonally. We cannot project 3D directions perspectively because they have no fixed position and the perspective position depends on the position.

Parameters:

• dir
  • a dir3 in the reference space.
• plane
  • a plane3 in the reference space. The image plane.

Returns:

• a dir2 on the image plane.

Aliases: affineplane.dir3.projectTo

Source: projectToPlane.js

affineplane.dir3.toSpherical(dir)

Get theta and phi angles of spherical coordinate system for the given direction. The two angles are unique for all directions. The function is compatible with affineplane.dir3.fromSpherical

Parameters:

• dir
  • a dir3 object or unit vec3.

Returns:

• an object with properties
  • theta
    • a number, an angle in radians on the xy-plane when
    • measured from positive x-axis and around z-axis.
    • In geographical terms, if z-axis points the north pole, a longitude.
    • In spherical coordinate system, this is often called azimuthal angle.
  • phi
    • a number, an angle in radians from the positive z-axis.
    • In geographical terms, a latitude if measured from the north pole.
    • In spherical coordinate system, this is often called the polar angle.

Source: toSpherical.js

affineplane.dir3.toVector(dir[, magn])

Parameters:

• dir
  • a dir3
• magn
  • optional number, default to 1. The magnitude of the vector to create.
  • Note that a negative magnitude creates a vector to opposite direction.

Returns:

• a vec3

Source: toVector.js

affineplane.dir3.transitFrom(dir, plane)

Represent the direction on the reference plane without losing information. Note that plane translation or scale does not affect direction.

Parameters:

• dir
  • a dir3 on the source plane.
• plane
  • a plane3 on the reference plane. The source plane.

Returns:

• a dir3, represented on the reference plane.

Source: transitFrom.js

affineplane.dir3.transitTo(dir, target)

Transit a dir3 to a target plane. In other words, represent the direction in the coordinate system of the target plane.

Parameters:

• dir
  • a number, a dir3 on the reference plane.
• target
  • a plane3, the target plane, represented on the reference plane.

Returns:

• a dir3, represented on the target plane.

Source: transitTo.js

affineplane.dir3.validate(d)

Check if object is a valid dir3. Valid dir3 is an object with properties x,y,z that represent a unit vector.

Parameters:

• d
  • an object

Returns:

• a boolean

Source: validate.js

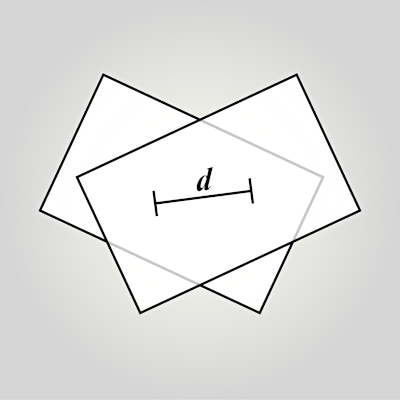
affineplane.dist2

The distance measure is a directionless, always positive number (≥0). If transited between bases, only a change in the coordinate scale affects the distance. Rotation or translation of the basis does not change the distance measure.

Contents:

• affineplane.dist2.almostEqual
• affineplane.dist2.create
• affineplane.dist2.equal
• affineplane.dist2.projectTo
• affineplane.dist2.projectToPlane
• affineplane.dist2.transitFrom
• affineplane.dist2.transitTo
• affineplane.dist2.validate

Source: dist2/index.js

affineplane.dist2.almostEqual(c, d[, tolerance])

Test if distances c, d are almost equal by the margin of tolerance.

Parameters:

• c
  • a number, the dist2
• d
  • a number, the dist2
• tolerance
  • optional number, default is affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.dist2.create(d)

Create a distance measure. Basically it is just the absolute value of the number.

Parameters:

• d
  • a number

Returns:

• a number, always zero or positive.

Source: create.js

affineplane.dist2.equal(c, d)

Test if distances c, d are strictly equal.

Parameters:

• c
  • a number, the dist2
• d
  • a number, the dist2

Returns:

• a boolean

Source: equal.js

affineplane.dist2.projectTo

Alias of affineplane.dist2.projectToPlane

affineplane.dist2.projectToPlane(dist, target[, camera])

Project a distance onto a target plane in 3D. The distance is assumed to be measured on the reference plane z=0. If camera is given, project perspectively. Otherwise, project orthogonally.

Parameters:

• dist
  • a dist2 in the reference basis.
• target
  • a plane3 in the reference basis.
• camera
  • optional point3 in the reference basis.

Returns:

• a dist2 on the target plane.

Aliases: affineplane.dist2.projectTo

Source: projectToPlane.js

affineplane.dist2.transitFrom(dist, source)

Transit a distance from the source basis to the reference basis.

Parameters:

• dist
  • a number, a dist2 distance measure in the source basis.
• source
  • a plane2, the source plane, represented in the reference basis.

Returns:

• a number, a dist2, represented on the reference basis.

Source: transitFrom.js

affineplane.dist2.transitTo(dist, target)

Transit a dist2 to another basis. In other words, represent the distance in the coordinate system of the target.

Parameters:

• dist
  • a number, a dist2 in the reference basis.
• target
  • a plane2, the target basis, represented in the reference basis.

Returns:

• a number, a dist2 in the target basis.

Source: transitTo.js

affineplane.dist2.validate(d)

Check if the argument is a valid dist2. Valid dist2 is a zero or positive number and not NaN.

Parameters:

• d
  • a value

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.dist3

The distance measure is a directionless, always positive number (≥0). When transited between bases, only a change in the coordinate scale affects the distance. Rotation or translation of the basis does not change the distance measure.

Contents:

• affineplane.dist3.almostEqual
• affineplane.dist3.create
• affineplane.dist3.equal
• affineplane.dist3.projectTo
• affineplane.dist3.projectToPlane
• affineplane.dist3.transitFrom
• affineplane.dist3.transitTo
• affineplane.dist3.validate

Source: dist3/index.js

affineplane.dist3.almostEqual(c, d[, tolerance])

Test if distances c, d are equal by the margin of tolerance.

Parameters:

• c
  • a number, the dist3
• d
  • a number, the dist3
• tolerance
  • optional number, default is affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.dist3.create(d)

Create a measure. Basically it is just the absolute value of the number.

Parameters:

• d
  • a number

Returns:

• a number, always zero or positive.

Source: create.js

affineplane.dist3.equal(c, d)

Test if distances c, d are strictly equal.

Parameters:

• c
  • a number, the dist3
• d
  • a number, the dist3

Returns:

• a boolean

Source: equal.js

affineplane.dist3.projectTo

Alias of affineplane.dist3.projectToPlane

affineplane.dist3.projectToPlane(dist, target[, camera])

Project a distance onto a target plane in 3D basis. The distance is assumed to be measured on the plane z=0 of the reference basis. If camera is given, project perspectively. Otherwise, project orthogonally. Note that when projected perspectively, only the change of scale in the perspective projection affects the distance.

Parameters:

• dist
  • a dist3 in the reference basis.
• target
  • a plane3 in the reference basis.
• camera
  • optional point3 in the reference basis.

Returns:

• a dist3 on the target plane.

Aliases: affineplane.dist3.projectTo

Source: projectToPlane.js

affineplane.dist3.transitFrom(dist, source)

Transit a distance from the source basis to the reference basis.

Parameters:

• dist
  • a dist3, represented in the source basis.
• source
  • a plane3, the source basis, represented in the reference basis.

Returns:

• a dist3, represented in the reference basis.

Source: transitFrom.js

affineplane.dist3.transitTo(dist, target)

Transit a dist3 to a target basis. In other words, represent the distance in the coordinate system of the basis.

Parameters:

• dist
  • a dist3 in the reference basis.
• target
  • a plane3, the target basis, represented in the reference basis.

Returns:

• a dist3 in the target basis.

Source: transitTo.js

affineplane.dist3.validate(d)

Check if the argument is a valid dist3. Valid dist3 is a zero or positive number and not NaN.

Parameters:

• d
  • a value

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.epsilon

Default margin for non-strict numeric equality. For example 0.0000000001.

Source: epsilon.js

affineplane.helm2

Provides functions for a special kind of 2D transformation matrices, two-dimensional Helmert transformations. These matrices represent translation, rotation, and uniform dilation. They are also known as affine non-reflective similarity transformations.

The functions expect the transformation as an object with properties { a, b, x, y }

Like vec2 and unlike point2, helm2 represents movement. Therefore it has no single position in space, and is not affected by plane translations. See affineplane.plane2 for a positional variant.

Contents:

• affineplane.helm2.addDilation
• affineplane.helm2.addRotation
• affineplane.helm2.almostEqual
• affineplane.helm2.almostEquals
• affineplane.helm2.clone
• affineplane.helm2.combine
• affineplane.helm2.compose
• affineplane.helm2.copy
• affineplane.helm2.create
• affineplane.helm2.det
• affineplane.helm2.determinant
• affineplane.helm2.equal
• affineplane.helm2.equals
• affineplane.helm2.fromArray
• affineplane.helm2.fromBasisVector
• affineplane.helm2.fromFeatures
• affineplane.helm2.fromPlane
• affineplane.helm2.fromPolar
• affineplane.helm2.fromVector
• affineplane.helm2.getDilation
• affineplane.helm2.getRotation
• affineplane.helm2.getScale
• affineplane.helm2.getTranslation
• affineplane.helm2.inverse
• affineplane.helm2.invert
• affineplane.helm2.limitDilation
• affineplane.helm2.multiply
• affineplane.helm2.projectTo
• affineplane.helm2.projectToCameraTransform
• affineplane.helm2.projectToPlane
• affineplane.helm2.rotateBy
• affineplane.helm2.scaleBy
• affineplane.helm2.setDilation
• affineplane.helm2.setRotation
• affineplane.helm2.setTranslation
• affineplane.helm2.setTranslation
• affineplane.helm2.snapRotation
• affineplane.helm2.solveLeft
• affineplane.helm2.solveRight
• affineplane.helm2.toArray
• affineplane.helm2.toMatrix
• affineplane.helm2.toString
• affineplane.helm2.transform
• affineplane.helm2.transitFrom
• affineplane.helm2.validate

Source: helm2/index.js

affineplane.helm2.addDilation(tr, delta)

Increase the scale multiplier of the transformation by addition. The rotation and translation properties are preserved.

Parameters:

• tr
  • a helm2
• delta
  • a number, the increment in scaling.

Returns:

• a helm2

Source: addDilation.js

affineplane.helm2.addRotation(tr, angle)

Increase rotation angle of the transformation by angle. The dilation and translation properties are preserved.

Parameters:

• tr
  • a helm2
• rotation
  • a number in radians

Returns:

• a helm2

Source: addRotation.js

affineplane.helm2.almostEqual(tr, ts[, epsilon])

Are two transforms almost equal? Return true if a matrix norm of the difference is smaller than epsilon. We use modified L1 norm aka Manhattan Distance to compute the difference.

Parameters:

• tr
  • a helm2, a transform
• ts
  • a helm2, a transform
• epsilon
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Aliases: affineplane.helm2.almostEquals

Source: almostEqual.js

affineplane.helm2.almostEquals

Alias of affineplane.helm2.almostEqual

affineplane.helm2.clone

Alias of affineplane.helm2.copy

affineplane.helm2.combine

Alias of affineplane.helm2.compose

affineplane.helm2.compose(tr, ts)

Multiply transformation matrix tr from the right with the given transformation matrix ts. In other words, transform the image of ts by tr.

Parameters:

• tr
  • a helm2
• ts
  • a helm2

Returns:

• a helm2

Aliases: affineplane.helm2.combine, affineplane.helm2.multiply

Source: compose.js

affineplane.helm2.copy(tr)

Parameters:

• tr
  • a helm2, a transform

Returns:

• a helm2, a transform

Aliases: affineplane.helm2.clone

Source: copy.js

affineplane.helm2.create(a, b, x, y)

Create a 2D non-reflective similarity transform object.

Parameters:

• a
  • a number. The diagonal of linear transformation.
• b
  • a number. The upper and lower triangle of lin. transf.
• x
  • a number. The translation towards x
• y
  • a number. The translation towards y

Returns:

• a helm2, a transform object

Source: create.js

affineplane.helm2.det(tr)

The matrix determinant of the transformation. If the determinant equals zero then the matrix cannot be inverted and thus is not a valid transformation. In practice, determinants close to zero are also problematic due to floating point arithmetics.

Parameters:

• tr
  • a helm2

Returns:

• a number, the determinant.

Aliases: affineplane.helm2.determinant

Source: det.js

affineplane.helm2.determinant(tr)

Alias of affineplane.helm2.det

affineplane.helm2.equal(tr, ts)

Are transforms exactly equal? Note that due to floating-point arithmetics, computation might cause exact equality to be broken. See affineplane.helm2.almostEqual for relaxed alternative.

Parameters:

• tr
  • a helm2, a transform
• ts
  • a helm2, a transform

Returns:

• a boolean

Aliases: affineplane.helm2.equals

Source: equal.js

affineplane.helm2.equals

Alias of affineplane.helm2.equal

affineplane.helm2.fromArray(abxy)

Create an affine similarity transform from 4-element array.

Parameters:

• abxy
  • an array with four number elements [a, b, x, y]

Returns:

• a helm2, a similarity transform.

Source: fromArray.js

affineplane.helm2.fromBasisVector(vec)

Create a linear transformation from the basis vector for x-axis. This uniquely determines the basis vector for y-axis, at 90 degrees clock-wise.

Parameters:

• vec
  • a vec2, the basis vector for x-axis.

Returns:

• a helm2, but with zero translation.

Source: fromBasisVector.js

affineplane.helm2.fromFeatures(feats)

Create a helm2 transformation from human-readable features.

Parameters:

• feats
  • object with properties:
    • dilation
      • a number, a multiplier
    • rotation
      • a number, in radians
    • translation
      • a vec2, the displacement vector

Returns:

• a helm2

Source: fromFeatures.js

affineplane.helm2.fromPlane(plane, origin)

Capture a Helmert transform from a plane. In other words, convert a passive affine transformation to an active one. The result answers to the task: create such Helmert transformation so that when applied to an identity plane at the given origin, it transforms the plane so that the result is equal to the given plane.

Parameters:

• plane
  • a plane2 on the reference plane
• origin
  • a point2 on the reference plane.

Returns:

• a helm2 on the reference plane

Source: fromPlane.js

affineplane.helm2.fromPolar(scale, rotation[, tx[, ty]])

Create a transform object by using scale magnitude, rotation angle, and translation.

Parameters:

• scale
  • a number, the scaling factor
• rotation
  • a number, rotation in radians from positive x-axis towards pos. y-axis.
• tx
  • optional number, translation toward positive x. Default 0.
• ty
  • optional number, translation toward positive y. Default 0.

Returns:

• a helm2, a transform object

Precondition:

• scale must be positive

Source: fromPolar.js

affineplane.helm2.fromVector(vec)

Create a helm2 transformation from a translation vector.

Parameters:

• vec
  • a vec2, the displacement vector

Returns:

• a helm2

Source: fromVector.js

affineplane.helm2.getDilation(tr)

Get the dilation component of the transformation.

Parameters:

• tr
  • a helm2

Returns:

• a number, the scale multiplier.

Aliases: affineplane.helm2.getScale

Source: getDilation.js

affineplane.helm2.getRotation(tr)

Get the rotation component of the transform in radians.

Parameters:

• tr
  • a helm2

Returns:

• a number, in radians

Source: getRotation.js

affineplane.helm2.getScale

Alias of affineplane.helm2.getDilation

affineplane.helm2.getTranslation(tr)

Get translation component of the transformation as a vector.

Parameters:

• tr
  • a helm2

Returns:

• a vec2

Source: getTranslation.js

affineplane.helm2.inverse(tr)

Alias of affineplane.helm2.invert

affineplane.helm2.invert(tr)

Invert the transform. A transform from B to C becomes a transform from C to B.

Parameters:

• tr
  • a helm2

Returns:

• a helm2, inversed transform

Aliases: affineplane.helm2.inverse

Source: invert.js

affineplane.helm2.limitDilation(tr, min, max)

Limit the dilating/scaling component of the transformation between min and max (inclusive).

Parameters:

• tr
  • a helm2, in the reference basis.
• min
  • a number, the minimum dilation relative to the reference basis. Must be positive.
• max
  • a number, the maximum dilation relative to the reference basis. Must be positive.

Returns:

• a helm2

Source: limitDilation.js

affineplane.helm2.multiply

Alias of affineplane.helm2.compose

affineplane.helm2.projectTo

Alias of affineplane.helm2.projectToPlane

affineplane.helm2.projectToCameraTransform(helm, origin, camera)

Convert the dilation in the transform to a translation of the camera, so that the plane would dilate the same amount due to the perspective. This can be used to convert pinch gestures to forward movement. Also invert rotation and translation for camera movement.

Parameters:

• helm
  • a helm2 in the reference basis. Applied at origin.
• origin
  • a point3 in the reference basis. Position of the transform.
• camera
  • a point3, in the reference basis.

Returns:

• a helm3, with scale of 1, in the reference basis.

Source: projectToCameraTransform.js

affineplane.helm2.projectToPlane(tr, plane[, camera])

Project transformation onto a plane. If camera is given, project perspectively. Projection does not affect the dilation or rotation property of the tr. Projection only affects the scale of the translation.

Parameters:

• tr
  • a helm2 on the reference plane z=0.
• plane
  • a plane3 in the reference space. The projection plane.
• camera
  • optional point3 in the reference space. The camera position. Set for perspective projection.

Returns:

• a helm2 on the projection plane.

Aliases: affineplane.helm2.projectTo

Source: projectToPlane.js

affineplane.helm2.rotateBy(tr, radians)

Rotate image of the transform by the given radians. This changes the direction of the translation but preserves the scaling and rotating effects.

Parameters:

• tr
  • a helm2, a transform
• radians
  • a number, angle in radians

Returns:

• a helm2, a transform

Source: rotateBy.js

affineplane.helm2.scaleBy(tr, multiplier)

Scale image of the transform by the given multiplier. Dilation and translation are multiplied, rotation and translation direction are preserved.

Parameters:

• tr
  • a helm2, a transform on the reference plane.
• multiplier
  • a number

Returns:

• a helm2, a transform

Source: scaleBy.js

affineplane.helm2.setDilation(tr, dilation)

Replace scaling of the transformation. The rotation and translation properties are preserved.

Parameters:

• tr
  • a helm2
• dilation
  • a number

Returns:

• a helm2

Source: setDilation.js

affineplane.helm2.setRotation(tr, angle)

Replace rotation angle of the transformation. The dilation and translation properties are preserved.

Parameters:

• tr
  • a helm2
• rotation
  • a number in radians

Returns:

• a helm2

Source: setRotation.js

affineplane.helm2.setTranslation(tr, vec)

Increase translation property of the transformation by a vector. The dilation and rotation properties are preserved.

Parameters:

• tr
  • a helm2
• vec
  • a vec2, the new translation vector

Returns:

• a helm2

Source: addTranslation.js

affineplane.helm2.setTranslation(tr, vec)

Replace translation property of the transformation. The dilation and rotation properties are preserved.

Parameters:

• tr
  • a helm2
• vec
  • a vec2, the new translation vector

Returns:

• a helm2

Source: setTranslation.js

affineplane.helm2.snapRotation(tr)

Round the rotation property of the transformation to nearest orthogonal angle 0, 90, 180, and 270 deg. Note that if the given transform has exact 45, 135, 225, or 315 deg rotation then the nearest orthogonal angle is arbitrarily either the next or previous orthogonal angle due to the variation caused by floating-point arithmetics.

Parameters:

• tr
  • a helm2

Returns:

• a helm2

Source: snapRotation.js

affineplane.helm2.solveLeft(tb, tc)

Given transforms B, C, find transform A, where AB = C. Given that B is invertible, then A = C * iB.

Parameters:

• tb
  • a helm2
• tc
  • a helm2

Returns:

• a helm2, a transform

Source: solveLeft.js

affineplane.helm2.solveRight(ta, tc)

Given the transforms A and C, find the transform B, where A * B = C. Given that A is invertible, then B = iA * C.

Parameters:

• ta
  • a helm2
• tc
  • a helm2

Returns:

• a helm2, a transform

Source: solveRight.js

affineplane.helm2.toArray(tr)

Returns: an array representation of the transformation. Compatible with affineplane.helm2.fromArray.

Parameters:

• tr
  • a helm2

Returns:

• an array, [a, b, x, y]

Source: toArray.js

affineplane.helm2.toMatrix(tr)

Get the similarity transformation matrix in the format common to other APIs, including:

• WebKitCSSMatrix alias DOMMatrix
• kld-affine
• MDN documentation in some parts

Parameters:

• tr
  • a helm2

Returns:

• { a, b, c, d, e, f }

Source: toMatrix.js

affineplane.helm2.toString(tr)

Convert the transformation to a string compatible with the CSS transform-function data type, for example matrix(1, 2, -2, 1, 3, 4). Together with affineplane.helm2.fromString(…), this method enables helm2 serialization to and from strings.

Parameters:

• tr
  • a helm2

Returns:

• a string, CSS transform

Source: toString.js

affineplane.helm2.transform(tr, ts)

Multiply transformation matrix tr from the left with the given transformation matrix ts. In other words, transform the image of tr by ts.

For multiplication from right, see affineplane.helm2.compose.

Parameters:

• tr
  • a helm2
• ts
  • a helm2

Returns:

• a helm2

Source: transform.js

affineplane.helm2.transitFrom(tr, plane)

Transit a helm2 from the source plane to the reference plane. Note that:

• scale and rotation of the plane affects only the translating property of helm2, so that the direction of translation is preserved.
• translation of the plane does not affect helm2 at all.
• scaling and rotation properties of helm2 are preserved as is.

Parameters:

• tr
  • a helm2 transformation on the source plane.
• plane
  • a plane2, the source plane, represented on the reference plane.

Returns:

• a helm2, represented on the reference plane.

Source: transitFrom.js

affineplane.helm2.validate(tr)

Check if object is a valid helm2.

Parameters:

• tr
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.helm3

Functions for a special 3D affine transformation that consists of a translation in 3D, rotation around z-axis, and uniform scaling, alias dilation. In other words, the transformation is a 3D Helmert transformation with a limited ability to rotate only about z-axis.

A helm3 is an object { a, b, x, y, z }

Like vec3 and unlike point3, helm3 represents movement. Therefore it has no single position in space, and is not affected by plane translations. See affineplane.plane3 for a positional variant.

Contents:

• affineplane.helm3.addDilation
• affineplane.helm3.addRotation
• affineplane.helm3.addTranslation
• affineplane.helm3.almostEqual
• affineplane.helm3.almostEquals
• affineplane.helm3.clone
• affineplane.helm3.combine
• affineplane.helm3.compose
• affineplane.helm3.copy
• affineplane.helm3.create
• affineplane.helm3.det
• affineplane.helm3.determinant
• affineplane.helm3.difference
• affineplane.helm3.equal
• affineplane.helm3.equals
• affineplane.helm3.fromArray
• affineplane.helm3.fromBasisVector
• affineplane.helm3.fromFeatures
• affineplane.helm3.fromPlane
• affineplane.helm3.fromVector
• affineplane.helm3.getDilation
• affineplane.helm3.getRotation
• affineplane.helm3.getScale
• affineplane.helm3.getTranslation
• affineplane.helm3.inverse
• affineplane.helm3.invert
• affineplane.helm3.limitDilation
• affineplane.helm3.projectTo
• affineplane.helm3.projectToPlane
• affineplane.helm3.rotateBy
• affineplane.helm3.scaleBy
• affineplane.helm3.setDilation
• affineplane.helm3.setRotation
• affineplane.helm3.setTranslation
• affineplane.helm3.toArray
• affineplane.helm3.toMatrix
• affineplane.helm3.transitFrom
• affineplane.helm3.transitTo
• affineplane.helm3.translateBy
• affineplane.helm3.validate

Source: helm3/index.js

affineplane.helm3.addDilation(tr, delta)

Increase the scale multiplier of the transformation by addition. The rotation and translation properties are preserved.

Parameters:

• tr
  • a helm3
• delta
  • a number, the increment in scaling.

Returns:

• a helm3

Source: addDilation.js

affineplane.helm3.addRotation(tr, angle)

Increase rotation angle of the transformation by an angle. The dilation and translation properties are preserved.

Parameters:

• tr
  • a helm3
• rotation
  • a number in radians

Returns:

• a helm3

Source: addRotation.js

affineplane.helm3.addTranslation(tr, vec)

Modify transformation so that its image is translated by the given vector. In other words it transforms points further by the given vector.

Parameters:

• tr
  • a helm3, a transform
• vec
  • a vec2 or vec3

Returns:

• a helm3, a transform

Aliases: affineplane.helm3.translateBy

Source: addTranslation.js

affineplane.helm3.almostEqual(tr, ts[, epsilon])

Are two transforms almost equal? Return true if a matrix norm of the difference is smaller than epsilon. We use modified L1 norm aka Manhattan Distance to compute the difference.

Parameters:

• tr
  • a helm3, a transform
• ts
  • a helm3, a transform
• epsilon
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean, true if equal

Aliases: affineplane.helm3.almostEquals

Source: almostEqual.js

affineplane.helm3.almostEquals

Alias of affineplane.helm3.almostEqual

affineplane.helm3.clone

Alias of affineplane.helm3.copy

affineplane.helm3.combine

Alias of affineplane.helm3.compose

affineplane.helm3.compose(tr, ts)

Multiply the helm3 matrix tr from the right with the helm3 matrix ts. In other words, transform the image of ts by tr.

Parameters:

• tr
  • a helm3
• ts
  • a helm3

Returns:

• a helm3

Aliases: affineplane.helm3.combine

Source: compose.js

affineplane.helm3.copy(tr)

Parameters:

• tr
  • a helm3, a transform

Returns:

• a helm3, a transform

Aliases: affineplane.helm3.clone

Source: copy.js

affineplane.helm3.create(a, b, x, y, z)

Create a new helm3 object.

Parameters:

• a
  • number, linear transform basis vector element
• b
  • number, linear transform basis vector element
• x
  • number, change in horizontal position
• y
  • number, change in vertical position
• z
  • number, change in depth

Returns:

• a helm3

Source: create.js

affineplane.helm3.det(tr)

The matrix determinant of the transformation. If the determinant equals zero then the matrix cannot be inverted and thus is not a valid transformation. In practice, determinants close to zero are also problematic due to floating point arithmetics.

Parameters:

• tr
  • a helm3

Returns:

• a number, the determinant.

Aliases: affineplane.helm3.determinant

Source: det.js

affineplane.helm3.determinant(tr)

Alias of affineplane.helm3.det

affineplane.helm3.difference(h, hh)

Compute a transformation that maps the codomain of hh to the codomain of h. In other words, find transformation T such that Thh = h <=> T = hinv(hh). The result is the difference between the transformations h and hh.

Parameters:

• h
  • a helm3
• hh
  • a helm3

Returns:

• a helm3

Source: difference.js

affineplane.helm3.equal(tr, ts)

True if transformations are exactly equal. Note that due to floating-point arithmetics, computation might cause exact equality to be broken. See affineplane.helm3.almostEqual for a relaxed alternative.

Parameters:

• tr
  • a helm3, a transform
• ts
  • a helm3, a transform

Returns:

• a boolean

Aliases: affineplane.helm3.equals

Source: equal.js

affineplane.helm3.equals

Alias of affineplane.helm3.equal

affineplane.helm3.fromArray(arr)

Create an affine similarity transform from 5-element array.

Parameters:

• arr
  • an array of five numbers [a, b, x, y, z]

Returns:

• a helm3

Source: fromArray.js

affineplane.helm3.fromBasisVector(vec)

Create a linear transformation from the basis vector for x-axis. This basis vector is limited to 2D and does not have z-component. This uniquely determines the basis vector for y-axis, at 90 degrees clock-wise, and consequently the z-axis according to the right-hand rule.

Parameters:

• vec
  • a vec2, the basis vector for x-axis in the xy-plane of the reference basis.

Returns:

• a helm2z, but with zero translation.

Source: fromBasisVector.js

affineplane.helm3.fromFeatures(feats)

Create a helm3 transformation from human-readable features.

Parameters:

• feats
  • object with properties:
    • dilation
      • a number, a scale multiplier
    • rotation
      • a number, delta angle in radians
    • translation
      • a vec3, the displacement vector

Returns:

• helm3

Source: fromFeatures.js

affineplane.helm3.fromPlane(plane, origin)

Capture a Helmert transform from a plane. In other words, convert a passive affine transformation to an active one. The result answers to the task: create such Helmert transformation so that when applied to an identity plane at the given origin, it transforms the plane so that the result is equal to the given plane.

Parameters:

• plane
  • a plane3 on the reference plane
• origin
  • a point3 on the reference plane.

Returns:

• a helm3 on the reference plane

Source: fromPlane.js

affineplane.helm3.fromVector(vec)

Create a helm3 transformation from a translation vector.

Parameters:

• vec
  • a vec3, the displacement vector

Returns:

• a helm3

Source: fromVector.js

affineplane.helm3.getDilation(tr)

Get the dilation component of the transformation.

Parameters:

• tr
  • a helm3

Returns:

• a number, the scale multiplier.

Aliases: affineplane.helm3.getScale

Source: getDilation.js

affineplane.helm3.getRotation(tr)

Get the rotation component of the transform in radians. This is rotation around z-axis to right hand direction.

Parameters:

• tr
  • a helm3

Returns:

• a number, angle in radians

Source: getRotation.js

affineplane.helm3.getScale

Alias of affineplane.helm3.getDilation

affineplane.helm3.getTranslation(tr)

Get translation component of the transformation as a vector.

Parameters:

• tr
  • a helm3

Returns:

• a vec3

Source: getTranslation.js

affineplane.helm3.inverse(tr)

Alias of affineplane.helm3.invert

affineplane.helm3.invert(tr)

Invert the transform. A transform from B to C becomes a transform from C to B.

Parameters:

• tr
  • a helm3

Returns:

• a helm3, inversed transform

Aliases: affineplane.helm3.inverse

Source: invert.js

affineplane.helm3.limitDilation(tr, min, max)

Limit the dilating/scaling component of the transformation between min and max (inclusive).

Parameters:

• tr
  • a helm3, in the reference basis.
• min
  • a number, the minimum dilation measured in the reference basis. Must be positive.
• max
  • a number, the maximum dilation measured in the reference basis. Must be positive.

Returns:

• a helm3

Source: limitDilation.js

affineplane.helm3.projectTo

Alias of affineplane.helm3.projectToPlane

affineplane.helm3.projectToPlane(tr, plane)

Project transformation onto a plane orthogonally. The transformation loses z translation.

Parameters:

• tr
  • a helm3 in the reference space.
• plane
  • a plane3 in the reference space. The image plane.

Returns:

• a helm2 on the image plane.

Aliases: affineplane.helm3.projectTo

Source: projectToPlane.js

affineplane.helm3.rotateBy(tr, radians)

Rotate image of the transform by the given radians around z-axis. This rotates the direction of the translation but preserves the scaling and rotating effects as well as the translation along z.

Parameters:

• tr
  • a helm3, a transform
• radians
  • a number, angle in radians

Returns:

• a helm3, a transform

Source: rotateBy.js

affineplane.helm3.scaleBy(tr, multiplier)

Scale image of the transform by the given multiplier. Dilation and translation are multiplied, rotation and translation direction are preserved. Note that also translation along z becomes multiplied.

Parameters:

• tr
  • a helm3, a transform on the reference plane.
• multiplier
  • a number

Returns:

• a helm3, a transform

Source: scaleBy.js

affineplane.helm3.setDilation(tr, dilation)

Replace scaling of the transformation. The rotation and translation properties are preserved.

Parameters:

• tr
  • a helm3
• dilation
  • a number

Returns:

• a helm3

Source: setDilation.js

affineplane.helm3.setRotation(tr, angle)

Replace rotation angle of the transformation. The dilation and translation properties are preserved.

Parameters:

• tr
  • a helm3
• rotation
  • a number in radians

Returns:

• a helm3

Source: setRotation.js

affineplane.helm3.setTranslation(tr, vec)

Replace translation property of the transformation. The dilation and rotation properties are preserved.

Parameters:

• tr
  • a helm3
• vec
  • a vec3, the new translation vector

Returns:

• a helm3

Source: setTranslation.js

affineplane.helm3.toArray(tr)

Serializes the transformation into an array representation. Compatible with affineplane.helm3.fromArray.

Parameters:

• tr
  • a helm3

Returns:

• an array [a, b, x, y, z]

Source: toArray.js

affineplane.helm3.toMatrix(tr)

Get the transformation as a 4x4 homogeneous 3D transformation matrix, using indexing similar to MDN matrix3d article.

Parameters:

• tr
  • a helm3

Returns:

• an object with properties:
  • { a1, a2, a3, a4, b1, b2, b3, b4, c1, c2, c3, c4 d1, d2, d3, d4 }

Elements are constructed like this:

┌                      ┐   ┌             ┐
│ tr.a -tr.b  0   tr.x │   │ a1 a2 a3 a4 │
│ tr.b  tr.a  0   tr.y │ = │ b1 b2 b3 b4 │
│ 0     0     m   tr.z │   │ c1 c2 c3 c4 │
│ 0     0     0   1    │   │ d1 d2 d3 d4 │
└                      ┘   └             ┘
where m = sqrt(tr.a*tr.a + tr.b*tr.b)

Source: toMatrix.js

affineplane.helm3.transitFrom(tr, source)

Transit a helm3 from the source plane to the reference plane.

Parameters:

• tr
  • a helm3 transformation on the source plane.
• source
  • a plane3, the source plane, represented on the reference plane.

Returns:

• a helm3, represented on the reference plane.

Invariants:

• scale and rotation of the plane affects only the translating property of helm3, so that the direction of translation is preserved.
• translation of the plane does not affect helm3 at all.
• scaling and rotation properties of helm3 are preserved as is.

Source: transitFrom.js

affineplane.helm3.transitTo(tr, target)

Transit a helm3 to a target plane. In other words, represent the helm3 in the coordinate system of the plane.

Parameters:

• tr
  • a helm3 transformation represented on the reference plane.
• target
  • a plane3, the target plane, represented on the reference plane.

Returns:

• a helm3, represented on the target plane.

Source: transitTo.js

affineplane.helm3.translateBy

Alias of affineplane.helm3.addTranslation

affineplane.helm3.validate(tr)

Check if object is a valid helm3.

Parameters:

• tr
  • an object

Returns:

• a boolean, true if valid helm3

Source: validate.js

affineplane.line2

Directed line object with origin point in space and a spanning vector.

A line2 is an object { origin: {x,y}, span: {x,y} }

Contents:

• affineplane.line2.at
• affineplane.line2.create
• affineplane.line2.fromPoints
• affineplane.line2.intersection
• affineplane.line2.normal
• affineplane.line2.validate

Source: line2/index.js

affineplane.line2.at(line, c)

Get a point on the line at position c from the line origin. For example c=2 gives a point at two spanning vectors away from the origin.

Parameters:

• line
  • a line2
• c
  • a number, one-dimensional coordinate along the line

Returns:

• a point2

Source: at.js

affineplane.line2.create(origin, span)

Create a line from an origin point and a spanning vector.

Parameters:

• origin
  • a point2
• span
  • a vec2, the line spanning vector. Defines the unit on the line.

Returns:

• a line2

Source: create.js

affineplane.line2.fromPoints(p, q)

Create a line from two points with a spanning vector from p to q.

Parameters:

• p
  • a point2
• q
  • a point2

Returns:

• a line2

Source: fromPoints.js

affineplane.line2.intersection(l, ll)

Find intersection point between two lines, if any. If the lines are parallel but not equal, no intersection exist and therefore the result is null. If the lines are equal, while the whole line would be the true intersection, the result is the origin point of the first line.

Parameters:

• l
  • a line2
• ll
  • a line2

Returns:

• a point2 or null

Source: intersection.js

affineplane.line2.normal(line)

Get a normal vector for the line. It is perpendicular to the line. Note that a line has two normal vectors, one for each side. The returned normal is the one at the right hand.

Parameters:

• line
  • a line2

Returns:

• a vec2, a vector perpendicular to the line.

Source: normal.js

affineplane.line2.validate(obj)

Check if the object is a valid line2. Valid line2 has origin and span properties that are valid point2 and vec2, respectively.

Parameters:

• obj
  • an object, the line candidate.

Returns:

• a boolean, true if valid line2

Source: validate.js

affineplane.line3

Directed line object in 3D, Represented as an origin point and a spanning vector.

A line3 is an object { origin: {x,y,z}, span: {x,y,z} }

Contents:

• affineplane.line3.at
• affineplane.line3.create
• affineplane.line3.fromPoints
• affineplane.line3.intersection
• affineplane.line3.validate

Source: line3/index.js

affineplane.line3.at(line, c)

Get a point on the line at position c from the line origin. For example c=2 gives a point at two spanning vectors away from the origin.

Parameters:

• line
  • a line3
• c
  • a number

Returns:

• a point3

Source: at.js

affineplane.line3.create(origin, span)

Create a 3d line from an origin point and a spanning vector.

Parameters:

• origin
  • a point3
• span
  • a vec3, the line spanning vector. Defines the unit on the line.

Returns:

• a line3

Source: create.js

affineplane.line3.fromPoints(p, q)

Create a line from two points with a spanning vector from p to q.

Parameters:

• p
  • a point3
• q
  • a point3

Returns:

• a line3

Source: fromPoints.js

affineplane.line3.intersection(l, ll)

Find intersection point between two lines, if any. If the lines are parallel but not equal, or the lines are skew, no intersection exist and therefore the result is null. If the lines are equal, while the whole line would be the true intersection. However, in this case we pick the origin point of the first line.

Parameters:

• l
  • a line3
• ll
  • a line3

Returns:

• a point3 or null

Source: intersection.js

affineplane.line3.validate(line)

Check if the object is a valid line3. Valid line3 has origin and span properties that are valid point3 and vec3, respectively.

Parameters:

• line
  • an object

Returns:

• a boolean, true if valid line2

Source: validate.js

affineplane.orient2

Orientation in 2D. Represented by an object { a, b }.

Contents:

• affineplane.orient2.almostEqual
• affineplane.orient2.create
• affineplane.orient2.fromPolar
• affineplane.orient2.fromVector
• affineplane.orient2.transitFrom
• affineplane.orient2.transitTo
• affineplane.orient2.validate

Source: orient2/index.js

affineplane.orient2.almostEqual(p, q[, tolerance])

Test if two orientations are almost equal within the tolerance.

Parameters:

• p
  • an orient2
• q
  • an orient2
• tolerance
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.orient2.create(a, b)

Parameters:

• a
  • a number
• b
  • a number

Returns:

• a orient2

Source: create.js

affineplane.orient2.fromPolar(direction)

Create an orientation from angle or vector.

Parameters:

• direction
  • a number, the azimuth angle in radians.
  • a dir2
  • a vec2

Returns:

• an orient2

Aliases: affineplane.orient2.fromVector

Source: fromPolar.js

affineplane.orient2.fromVector(vec)

Alias of affineplane.orient2.fromPolar

affineplane.orient2.transitFrom(r, source)

Transit an orientation from the source basis to the reference basis.

Parameters:

• r
  • a orient2 in the source basis.
• source
  • a plane2, the source basis, represented in the reference basis.

Returns:

• a orient2, represented in the reference basis.

Source: transitFrom.js

affineplane.orient2.transitTo(r, target)

Transit a orient2 to a target basis. In other words, represent the direction in the coordinate system of the target basis.

Parameters:

• r
  • a number, a orient2 in the reference basis.
• target
  • a plane2, the target basis, represented in the reference basis.

Returns:

• a orient2 in the target basis.

Source: transitTo.js

affineplane.orient2.validate(r)

Check if the object is a valid orient2. Valid object has properties a and b which represent valid rotation matrix.

Parameters:

• r
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.path2

Two-dimensional path; Array of point2; Open sequence of points; Does not form a polygon but a sequence of line segments.

Example: [{ x, y }, { x, y }, ...]

Contents:

• affineplane.path2.combine
• affineplane.path2.create
• affineplane.path2.transitFrom
• affineplane.path2.transitTo
• affineplane.path2.validate

Source: path2/index.js

affineplane.path2.combine(pa, pb)

Combine paths together.

Parameters:

• pa
  • a path2
• pb
  • a path2

Returns:

• a path2

Source: combine.js

affineplane.path2.create(points)

Create a path on plane. Deep-clones the points array.

Parameters:

• points
  • array of point2

Returns:

• a path2, array of points

Source: create.js

affineplane.path2.transitFrom(path, source)

Represent a path on the reference basis.

Parameters:

• path
  • a path2, represented on the source basis.
• source
  • a plane2, the source basis, represented on the reference basis.

Returns:

• a path2, represented on the reference basis.

Source: transitFrom.js

affineplane.path2.transitTo(path, target)

Transit a path to the target basis.

Parameters:

• path
  • a path2, on the reference basis.
• target
  • a plane2, the target basis, represented on the reference basis.

Returns:

• a path2, represented on the target basis.

Source: transitTo.js

affineplane.path2.validate(p)

Check if the object is a valid path2. A valid path2 is an array of valid point2 objects.

Parameters:

• p
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.path3

Three-dimensional path; Array of point3; Open sequence of points; Does not form a polygon but a sequence of line segments.

Example: [{ x, y, z }, { x, y, z }, ...]

Contents:

• affineplane.path3.combine
• affineplane.path3.create
• affineplane.path3.projectTo
• affineplane.path3.projectToPlane
• affineplane.path3.transitFrom
• affineplane.path3.transitTo
• affineplane.path3.validate

Source: path3/index.js

affineplane.path3.combine(pa, pb)

Combine paths together.

Parameters:

• pa
  • a path3
• pb
  • a path3

Returns:

• a path3

Source: combine.js

affineplane.path3.create(points)

Create a path on plane. Deep-clones the points array.

Parameters:

• points
  • array of point3

Returns:

• a path3, array of points

Source: create.js

affineplane.path3.projectTo

Alias of affineplane.path3.projectToPlane

affineplane.path3.projectToPlane(path, plane[, camera])

Project a 3D path onto a 2D plane orthogonally. Project perspectively if a camera position is given.

Parameters:

• path
  • a path3, in the reference basis.
• plane
  • a plane3, in the reference basis. The image plane to which to project.
• camera
  • a point3, in the reference basis. The location of the camera.

Returns:

• a path2 on the image plane.

Aliases: affineplane.path3.projectTo

Source: projectToPlane.js

affineplane.path3.transitFrom(path, source)

Represent a path on the reference basis.

Parameters:

• path
  • a path3, represented on the source basis.
• source
  • a plane3, the source basis, represented on the reference basis.

Returns:

• a path3, represented on the reference basis.

Source: transitFrom.js

affineplane.path3.transitTo(path, target)

Transit a path to the target basis.

Parameters:

• path
  • a path3, on the reference basis.
• target
  • a plane3, the target basis, represented on the reference basis.

Returns:

• a path3, represented on the target basis.

Source: transitTo.js

affineplane.path3.validate(p)

Check if the object is a valid path3. A valid path3 is an array of valid point3 objects.

Parameters:

• p
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.plane2

A 2D euclidean plane.

A plane is a 2D Helmert transformation from the plane coordinates to a reference coordinate system called the reference plane. The transform defines the scale and angle of the plane and its origin position on the reference.

The plane is represented with an object { a, b, x, y }. See the illustration below for visual explanation of these properties.

For example { a: 1, b: 0, x: 0, y: 0 } defines a plane is an exact copy of its reference plane. For another example { a: 1, b: 0, x: 20, y: 0 } defines a plane which is located +20 units along x-axis of the reference plane.

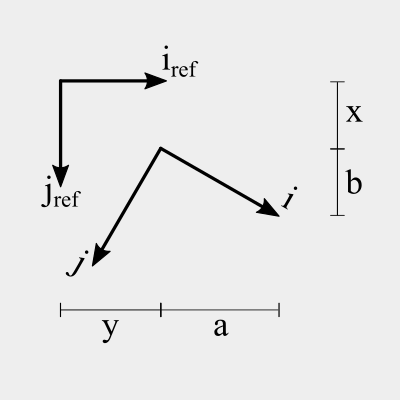
Contents:

• affineplane.plane2.IDENTITY
• affineplane.plane2.almostEqual
• affineplane.plane2.at
• affineplane.plane2.between
• affineplane.plane2.compose
• affineplane.plane2.copy
• affineplane.plane2.create
• affineplane.plane2.difference
• affineplane.plane2.equal
• affineplane.plane2.fromFeatures
• affineplane.plane2.fromHelmert
• affineplane.plane2.getScale
• affineplane.plane2.invert
• affineplane.plane2.limitScale
• affineplane.plane2.orientation
• affineplane.plane2.projectTo
• affineplane.plane2.projectToPlane
• affineplane.plane2.rotateBy
• affineplane.plane2.rotateTo
• affineplane.plane2.rotateToOrtho
• affineplane.plane2.scaleBy
• affineplane.plane2.scaleTo
• affineplane.plane2.transform
• affineplane.plane2.transformInside
• affineplane.plane2.transitFrom
• affineplane.plane2.transitTo
• affineplane.plane2.translateBy
• affineplane.plane2.translateTo
• affineplane.plane2.validate

Source: plane2/index.js

affineplane.plane2.IDENTITY

The identity plane is identical to its reference plane.

Source: plane2/index.js

affineplane.plane3.IDENTITY

The identity plane is identical to its reference plane.

Source: plane3/index.js

affineplane.plane2.almostEqual(pa, pb[, tolerance])

Test if two planes are almost equal.

Parameters:

• pa
  • a plane2
• pb
  • a plane2
• tolerance
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.plane2.at(plane, x, y)

Take a point on the plane and transit it to the reference basis.

Parameters:

• plane
  • a plane2, in the reference basis.
• x
  • a number, the horizontal coordinate on the plane
• y
  • a number, the vertical coordinate on the plane

Returns:

• a point2 in the reference basis.

Source: at.js

affineplane.plane2.between

Alias of affineplane.plane2.difference

affineplane.plane2.compose(planea, planeb)

Combine two planes together.

Parameters:

• planea
  • a plane2 on the reference plane
• planeb
  • a plane2 on the planea

Returns:

• a plane2 on the reference plane

Source: compose.js

affineplane.plane2.copy(plane)

Clone the plane object.

Parameters:

• plane
  • a plane2

Returns:

• a plane2

Source: copy.js

affineplane.plane2.create(origin, span)

Create a plane2 from an origin point and a basis vector.

Parameters:

• origin
  • a point2 on the reference plane.
• span
  • a vec2 on the reference plane. This vector is the basis vector for the x-axis of the plane. The basis vector for y can be found 90deg clockwise from x-axis.

Returns:

• a plane2

Source: create.js

affineplane.plane2.difference(p, pp)

Find the difference between two planes. In other words, compute such transformation T that maps the plane pp to the plane p.

Parameters:

• p
  • a plane2, in the reference basis.
• pp
  • a plane2, in the reference basis.

Returns:

• a helm2, in the reference basis.

Aliases: affineplane.plane2.between

Source: difference.js

affineplane.plane2.equal(p1, p2)

Test if two planes are strictly equal in their properties. See affineplane.plane2.almostEqual for a relaxed alternative.

Parameters:

• p1
  • a plane2
• p2
  • a plane2

Returns:

• a boolean

Source: equal.js

affineplane.plane2.fromFeatures(feats)

Create a plane from human readable features.

Parameters:

• feats
  • an object with optional props:
    • angle
      • a number, angle in radians with respect to the reference plane.
    • scale
      • a number, scale multiplier with respect to the reference plane.
    • origin
      • a point2, the plane origin point on the reference plane.

Returns:

• a plane2

Source: fromFeatures.js

affineplane.plane2.fromHelmert(tr, origin)

Create a plane by transforming an identity plane about the given transform origin. For example, you can create a plane that has been rotated around a point (100, 100). The choice of transform origin does not affect scale or rotation of the created plane but does affect its translative component.

Parameters:

• tr
  • a helm2 on the reference plane
• origin
  • a point2 on the reference plane

Returns:

• a plane2 on the reference plane

Source: fromHelmert.js

affineplane.plane2.getScale(plane)

The length of the vector.

Parameters:

• plane
  • a plane2 on the reference plane

Returns:

• a number, the scale multiplier with respect to the reference plane.

Source: getScale.js

affineplane.plane2.invert(plane)

A plane is a mapping from the plane’s coordinates onto the reference plane. The inversion of the plane switches the roles so that the result is the reference plane, represented in the coordinates of the given plane.

Parameters:

• plane
  • a plane2, the plane to invert represented on the reference plane.

Returns:

• a plane2, the reference plane represented on the given plane.

Source: invert.js

affineplane.plane2.limitScale(plane, min, max)

Limit the scale the plane transformation between min and max (inclusive).

Parameters:

• plane
  • a plane2, in the reference basis.
• min
  • a number, the minimum scale measured in the reference basis. Must be positive.
• max
  • a number, the maximum scale measured in the reference basis. Must be positive.

Returns:

• a plane2

Source: limitScale.js

affineplane.plane2.orientation(plane)

The orientation of the plane, i.e. the rotation from default. If the plane is singular, falls back to the default orientation.

Parameters:

• plane
  • a plane2, in the reference basis

Returns:

• a orient2, in the reference basis

Source: orientation.js

affineplane.plane2.projectTo

Alias of affineplane.plane2.projectToPlane

affineplane.plane2.projectToPlane(plane, target[, camera])

Project a 2D plane from reference to the target parallel 2D plane in 3D. If camera is given, project perspectively, otherwise orthogonally.

Parameters:

• plane
  • a plane2 in the reference space, z=0.
• target
  • a plane3 in the reference space. The image plane to which to project.
• camera
  • optional point3 in the reference space.

Returns:

• a plane2 on the image plane.

Aliases: affineplane.plane2.projectTo

Source: projectToPlane.js

affineplane.plane2.rotateBy(plane, center, radians)

Rotate the given plane on the reference plane around a center point.

Parameters:

• plane
  • a plane2 on the reference plane. The plane to rotate.
• center
  • a point2, a point on the reference plane.
• radians
  • a number, angle in radians, direction x->y.

Returns:

• a plane2 on the reference plane after rotation.

Source: rotateBy.js

affineplane.plane2.rotateTo(plane, center, radians)

Rotate the plane around a point so that after the rotation, the x-axis of the plane points to the given direction. The center point stays fixed during the operation.

Parameters:

• plane
  • a plane2, the plane to rotate. Represented on the reference plane.
• center
  • a point2, the point around which to rotate. Represented on the reference plane.
• radians
  • a number, angle to rotate to. Relative to the reference plane x-axis.

Returns:

• a plane2, the plane after rotation.

Source: rotateTo.js

affineplane.plane2.rotateToOrtho(plane, center)

Rotate plane to nearest orthogonal angle 0, 90, 180, and 270 deg with respect to the reference plane.

Parameters:

• plane
  • a plane2 to rotate.
• center
  • a point2, a point on the reference plane. The rotation center.

Returns:

• a plane2

Note that if the plane is at the middle of two ortho angles, namely at 45, 135, 225, or 315 deg, then the nearest orthogonal angle is arbitrarily either the next or previous orthogonal angle due to the small variations caused by floating-point arithmetics.

Source: rotateToOrtho.js

affineplane.plane2.scaleBy(plane, center, multiplier)

Create a plane that is scaled by the multiplier around a center point. For example, if a plane with basis vectors ex = (1,0), ey = (0,1) is scaled by 2, the basis vectors of the new plane are ex_hat = (2,0), ey_hat = (0,2).

Parameters:

• plane
  • a plane2 on the reference plane
• center
  • a point2 on the reference plane
• multiplier
  • a number, the scaling factor

Returns:

• a plane2, a scaled plane

Source: scaleBy.js

affineplane.plane2.scaleTo(plane, center, scale)

Create a plane that has the given scale. This is achieved by scaling the plane around a center point so that afterwards the plane scale becomes the desired scale.

Parameters:

• plane
  • a plane2 on the reference plane
• center
  • a point2 on the reference plane
• scale
  • a number, the desired scale

Returns:

• a plane2, a scaled plane

Source: scaleTo.js

affineplane.plane2.transform(plane, tr[, origin])

Transform the plane with a helmert transformation applied at origin.

Parameters:

• plane
  • a plane2 on the reference basis
• tr
  • a helm2 on the reference basis
• origin
  • optional point2 on the reference basis. Default {x:0,y:0}. The transformation will be applied to the plane at this point.

Returns:

• a plane2 on the reference plane

Source: transform.js

affineplane.plane2.transformInside(plane, tr[, origin])

Transform the plane with a Helmert transformation applied at the origin. Same as affineplane.plane2.transform except the transform and the origin are represented on the plane instead of the reference basis.

Parameters:

• plane
  • a plane2 on the reference basis
• tr
  • a helm2 on the plane
• origin
  • optional point2 on the plane. Default {x:0,y:0}. The transformation will be applied to the plane at this point.

Returns:

• a plane2 on the reference plane

Source: transformInside.js

affineplane.plane2.transitFrom(plane, source)

Transit a plane2 from the source plane to the reference plane. In other words, represent the plane in the coordinate system of the reference plane instead of the source plane.

Parameters:

• plane
  • a plane2 on the source plane.
• source
  • a plane2, the source plane, represented on the reference plane.

Returns:

• a plane2, represented on the reference plane.

Source: transitFrom.js

affineplane.plane2.transitTo

Transit a plane2 to a target plane. In other words, represent the plane2 in the coordinate system of the target plane.

Parameters:

• plane
  • a plane2 on the reference plane.
• target
  • a plane2, the target plane, represented on the reference plane.

Returns:

• a plane2, represented on the target plane.

Source: transitTo.js

affineplane.plane2.translateBy(plane, vec)

Translate the plane by a vector. Basically this moves the plane origin on the reference plane.

Parameters:

• plane
  • a plane2 on the reference plane.
• vec
  • a vec2, the translation vector. Represented on the reference plane.

Returns:

• a plane2 on the reference plane.

Source: translateBy.js

affineplane.plane2.translateTo(plane, p)

Move the plane origin to a new point. This translates the plane to a new position.

Parameters:

• plane
  • a plane2 on the reference plane
• p
  • a point2 on the reference plane

Returns:

• a plane2

Source: translateTo.js

affineplane.plane2.validate(plane)

Check if object is a valid plane2.

Parameters:

• plane
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.plane3

A plane3 does not model any possible plane in 3D space, but is limited to xy planes perpendicular to z-axis and with a known z position. Additionally, plane3 models orientation around z-axis and uniform scale in all three dimensions.

In other words, a plane is a helmert transform (helm3) from the plane coordinates to a reference coordinate system. Unlike helm3, the plane3 has position in the space. Therefore it can be projected perspectively.

The plane is represented with an object { a, b, x, y, z }

For example { a: 1, b: 0, x: 0, y: 0, z: 0 } is an exact copy of its reference plane. For another example { a: 1, b: 0, x: 20, y: 0, z: 0 } is +20 units along x-axis relative to its reference plane.

Contents:

• affineplane.plane3.IDENTITY
• affineplane.plane3.almostEqual
• affineplane.plane3.at
• affineplane.plane3.between
• affineplane.plane3.compose
• affineplane.plane3.copy
• affineplane.plane3.create
• affineplane.plane3.difference
• affineplane.plane3.equal
• affineplane.plane3.fromFeatures
• affineplane.plane3.fromHelmert
• affineplane.plane3.getNormal
• affineplane.plane3.getScale
• affineplane.plane3.invert
• affineplane.plane3.limitScale
• affineplane.plane3.orientation
• affineplane.plane3.projectByDepth
• affineplane.plane3.projectTo
• affineplane.plane3.projectToDepth
• affineplane.plane3.projectToPlane
• affineplane.plane3.projectToScale
• affineplane.plane3.rotateBy
• affineplane.plane3.rotateTo
• affineplane.plane3.rotateToOrtho
• affineplane.plane3.scaleBy
• affineplane.plane3.scaleTo
• affineplane.plane3.transform
• affineplane.plane3.transformBy
• affineplane.plane3.transformInside
• affineplane.plane3.transitFrom
• affineplane.plane3.transitTo
• affineplane.plane3.translateBy
• affineplane.plane3.translateTo
• affineplane.plane3.validate

Source: plane3/index.js

affineplane.plane3.almostEqual(pa, pb[, tolerance])

Test if two planes are almost equal.

Parameters:

• pa
  • a plane3
• pb
  • a plane3
• tolerance
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.plane3.at(plane, x, y, z)

Take a point relative to the plane and transit it to the reference basis.

Parameters:

• plane
  • a plane3, in the reference basis.
• x
  • a number, the horizontal coordinate on the plane
• y
  • a number, the vertical coordinate on the plane
• z
  • a number, the depth offset relative to the plane

Returns:

• a point3 in the reference basis.

Source: at.js

affineplane.plane3.between

Alias of affineplane.plane3.difference

affineplane.plane3.compose(planea, planeb)

Combine two planes together.

Parameters:

• planea
  • a plane3 on the reference plane. This plane maps from plane A to the reference plane.
• planeb
  • a plane3 on the planea. This plane maps from plane B to plane A.

Returns:

• a plane3 on the reference plane. This plane maps from plane B to the reference plane.

Source: compose.js

affineplane.plane3.copy(plane)

Clone the plane object.

Parameters:

• plane
  • a plane3

Returns:

• a plane3

Source: copy.js

affineplane.plane3.create(origin, span)

Create a plane from 3D origin point and 2D basis vector.

Parameters:

• origin
  • a point3, the position of the plane origin in the reference space.
• span
  • a vec2, the basis vector for the x-axis. The basis for y-axis is always 90deg from x-axis, the direction determined by the right-hand rule where thumb is parallel with positive z-axis.

Returns:

• a plane3

Source: create.js

affineplane.plane3.difference(p, pp)

Find the difference between the two planes. In other words, compute a transformation that would map the plane pp to the plane p: T * pp = p <=> T = p * inv(pp)

To represent planes on each other, see affineplane.plane3.transitFrom and affineplane.plane3.transitTo.

Parameters:

• p
  • a plane3, in the reference basis.
• pp
  • a plane3, in the reference basis.

Returns:

• a helm3, a transformation, in the reference basis.

Aliases: affineplane.plane3.between

Source: difference.js

affineplane.plane3.equal(p1, p2)

Test if two planes are strictly equal in their properties. See affineplane.plane3.almostEqual for a relaxed alternative.

Parameters:

• p1
  • a plane3
• p2
  • a plane3

Returns:

• a boolean

Source: equal.js

affineplane.plane3.fromFeatures(feats)

Create a plane from human readable features.

Parameters:

• feats
  • an object with optional props
    • angle
      • a number, angle in radians with respect to the reference plane.
    • scale
      • a number, scale multiplier with respect to the reference plane.
    • origin
      • a point3, the plane origin point in the reference space.

Returns:

• a plane3

Source: fromFeatures.js

affineplane.plane3.fromHelmert(tr, origin)

Create a plane by applying a transformation to an identity plane at the given transform origin. For example, you can create a plane that has been scaled about a point (100, 100, 100). The choice of transform origin does not affect scale or rotation of the created plane but does affect its translative component. Note that any rotation is performed around such a line that is parallel to z-axis and goes through the given origin point.

Parameters:

• tr
  • a helm2z on the reference plane
• origin
  • a point3 on the reference plane.

Returns:

• a plane3 on the reference plane

Source: fromHelmert.js

affineplane.plane3.getNormal(plane)

Get a unit vector perpendicular to the plane.

Parameters:

• plane
  • a plane3 on the reference plane

Returns:

• a vec3, the plane normal vector.

Source: getNormal.js

affineplane.plane3.getScale(plane)

The length of the basis vector, the scale multiplier.

Parameters:

• plane
  • a plane3 on the reference plane

Returns:

• a number, the scale multiplier with respect to the reference plane.

Source: getScale.js

affineplane.plane3.invert(plane)

Parameters:

• plane
  • a plane3, represented on the reference plane.

Returns:

• a plane3, the reference plane represented on the given plane.

Source: invert.js

affineplane.plane3.limitScale(plane, min, max)

Limit the scale the plane transformation between min and max (inclusive).

Parameters:

• plane
  • a plane3, in the reference basis.
• min
  • a number, the minimum scale measured in the reference basis. Must be positive.
• max
  • a number, the maximum scale measured in the reference basis. Must be positive.

Returns:

• a plane3

Source: limitScale.js

affineplane.plane3.orientation(plane)

The orientation of the plane, i.e. the rotation from default. If the plane is singular, falls back to the default orientation.

Parameters:

• plane
  • a plane3, in the reference basis

Returns:

• a orient2, in the reference basis

Source: orientation.js

affineplane.plane3.projectByDepth(plane, origin, deltaDepth)

Project a plane so that it translates by the given delta depth from the origin. The plane is also scaled so that it would look similar from the origin point of view.

If the origin point is on the plane, not projection is made and the given plane is returned as-is.

Parameters:

• plane
  • a plane3 in the reference basis.
• origin
  • a point3 in the reference basis.
• deltaDepth
  • a number, can be negative.

Returns:

• a plane3 in the reference basis.

Source: projectByDepth.js

affineplane.plane3.projectTo

Alias of affineplane.plane3.projectToPlane

affineplane.plane3.projectToDepth(plane, depth, camera)

Project the plane to the given depth so that it still looks the same to the camera. The plane is scaled and translated to match the appearance.

Parameters:

• plane
  • a plane3 in the reference space.
• depth
  • a number, the z coordinate in the reference space. The resulting plane will have this for its z coordinate.
• camera
  • a point3 in the reference space.

Returns:

• a plane3 in the reference space.

Source: projectToDepth.js

affineplane.plane3.projectToPlane(plane, target[, camera])

Project the plane based on the image plane position and the optional camera position. If camera is given, project perspectively, otherwise orthogonally.

Parameters:

• plane
  • a plane3 in the reference space.
• target
  • a plane3 in the reference space. The image plane to which to project.
• camera
  • optional point3 in the reference space.

Returns:

• a plane2 on the image plane.

Aliases: affineplane.plane3.projectTo

Source: projectToPlane.js

affineplane.plane3.projectToScale(plane, scale, camera)

Project the plane to the given scale so that it still looks the same to the camera. The plane is scaled and translated to match the appearance. Can be used to perspectively convert plane scale to translation.

Parameters:

• plane
  • a plane3 in the reference space.
• scale
  • a number, the desired scale, represented in the reference space.
• camera
  • a point3 in the reference space.

Returns:

• a plane3 in the reference space

Source: projectToScale.js

affineplane.plane3.rotateBy(plane, center, radians)

Rotate the given plane in the reference space around a line parallel to z-axis and which goes through the given center point. The plane z depth is preserved.

Parameters:

• plane
  • a plane3 in the reference space. The plane to rotate.
• center
  • a point3, a point in the reference space. Defines the line around which to rotate.
• radians
  • a number, angle in radians, direction x -> y.

Returns:

• a plane3 on the reference plane after rotation.

Source: rotateBy.js

affineplane.plane3.rotateTo(plane, center, radians)

Rotate the plane around a line parallel to z-axis and which goes though the given center point. After the rotation, the x-axis of the plane points to the given direction. The point where the line intersects the plane stays fixed during the operation.

Parameters:

• plane
  • a plane3, the plane to rotate. Represented on the reference plane.
• center
  • a point3, the point that defines the line around which to rotate. Represented on the reference plane.
• radians
  • a number, angle to rotate to. Relative to the reference plane x-axis.

Returns:

• a plane3, the plane after rotation.

Source: rotateTo.js

affineplane.plane3.rotateToOrtho(plane, center)

Rotate plane to nearest orthogonal angle 0, 90, 180, and 270 deg with respect to the reference plane. The rotation happens on xy-plane, around the line parallel to z-axis and travelling through the given point.

Parameters:

• plane
  • a plane3 to rotate.
• center
  • a point3, a point in the reference space.
  • Determines the rotation center.

Returns:

• a plane2

Note that if the plane is at the middle of two ortho angles, namely at 45, 135, 225, or 315 deg, then the nearest orthogonal angle is arbitrarily either the next or previous orthogonal angle due to the small variations caused by floating-point arithmetics.

Source: rotateToOrtho.js

affineplane.plane3.scaleBy(plane, center, multiplier)

Create a plane that is scaled by the multiplier around a center point. The center point is allowed to be off the plane. The scaling is performed about this center point.

For example, if a plane P with basis vectors ex = (1,0,0), ey = (0,1,0), ez = (0,1,0) is scaled by 2, the basis vectors of the new plane P_hat are ex_hat = (2,0,0), ey_hat = (0,2,0), ez_hat = (0,0,2) meaning that 3 units on P_hat are 6 units on P.

Parameters:

• plane
  • a plane3 on the reference plane
• center
  • a point3 on the reference plane
• multiplier
  • a number, the scaling factor

Returns:

• a plane3, a scaled plane

Source: scaleBy.js

affineplane.plane3.scaleTo(plane, center, scale)

Scale a plane to the given scale towards the center point.

Parameters:

• plane
  • a plane3 on the reference plane
• center
  • a point3 on the reference plane
• scale
  • a number, the desired scale

Returns:

• a plane3, a scaled plane

Source: scaleTo.js

affineplane.plane3.transform(plane, tr[, origin])

Transform the plane with a helmert transformation applied at origin.

Parameters:

• plane
  • a plane3 on the reference basis
• tr
  • a helm2 or helm3 on the reference basis
• origin
  • optional point3 on the reference basis. Default {x:0,y:0,z:0}. The transformation will be applied to the plane at this point.

Returns:

• a plane3 on the reference basis

Aliases: affineplane.plane3.transformBy

Source: transform.js

affineplane.plane3.transformBy

Alias of affineplane.plane3.transform

affineplane.plane3.transformInside(plane, tr[, origin])

Transform the plane with a Helmert transformation applied at the origin. Same as affineplane.plane3.transform except the transform and the origin are represented on the plane instead of the reference basis.

Parameters:

• plane
  • a plane3 on the reference basis
• tr
  • a helm3 on the plane
• origin
  • optional point3 on the plane. Default {x:0,y:0,z:0}. The transformation will be applied to the plane at this point.

Returns:

• a plane3 on the reference plane

Source: transformInside.js

affineplane.plane3.transitFrom(plane, source)

Transit a plane3 from the source plane to the reference plane. In other words, represent the same plane in the coordinate system of the reference plane.

Parameters:

• plane
  • a plane3, represented on the source plane.
• source
  • a plane3, the source plane, represented on the reference plane.

Returns:

• a plane3, represented on the reference plane.

Source: transitFrom.js

affineplane.plane3.transitTo(plane, target)

Transit a plane3 to a target plane. In other words, represent the plane3 in the coordinate system of the target plane.

Parameters:

• plane
  • a plane3, represented on the reference plane.
• target
  • a plane3, the target plane, represented on the reference plane.

Returns:

• a plane3, represented on the target plane.

Source: transitTo.js

affineplane.plane3.translateBy(plane, vec)

Translate the plane by a vector. Basically this moves the plane origin on the reference plane by the given vector.

Parameters:

• plane
  • a plane3 in the reference space.
• vec
  • a vec2 or vec3 in the reference space.

Returns:

• a plane3 in the reference space.

Source: translateBy.js

affineplane.plane3.translateTo(plane, p)

Source: translateTo.js

affineplane.plane3.validate(plane)

Check if object is a valid plane3.

Parameters:

• plane
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.point2

A two-dimensional point. A point is a position in affine space. Due to affinity, two points cannot be added together, although the distance between and their mean can be computed. An affine space does not have origin; { x:0, y:0 } is not an origin.

Contents:

• affineplane.point2.ZERO
• affineplane.point2.almostEqual
• affineplane.point2.average
• affineplane.point2.copy
• affineplane.point2.create
• affineplane.point2.delta
• affineplane.point2.diff
• affineplane.point2.difference
• affineplane.point2.direction
• affineplane.point2.distance
• affineplane.point2.equal
• affineplane.point2.equals
• affineplane.point2.fromArray
• affineplane.point2.homothety
• affineplane.point2.mean
• affineplane.point2.move
• affineplane.point2.offset
• affineplane.point2.polarOffset
• affineplane.point2.projectByDistance
• affineplane.point2.projectTo
• affineplane.point2.projectToLine
• affineplane.point2.projectToPlane
• affineplane.point2.rotateBy
• affineplane.point2.toArray
• affineplane.point2.transform
• affineplane.point2.transformMany
• affineplane.point2.transitFrom
• affineplane.point2.transitTo
• affineplane.point2.translate
• affineplane.point2.validate
• affineplane.point2.vectorTo

Source: point2/index.js

affineplane.point2.ZERO

The zero point

Source: point2/index.js

affineplane.point2.almostEqual(p, q[, epsilon])

Test if points are almost equal by the margin of epsilon.

Parameters:

• p
  • a point2
• q
  • a point2
• epsilon
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.point2.average(ps)

Average of points.

Parameters:

• ps
  • array of point2

Returns:

• a point2

Aliases: affineplane.point2.mean

Source: average.js

affineplane.point2.copy(p)

Copy point object.

Parameters:

• p
  • a point2

Returns:

• a point2

Source: copy.js

affineplane.point2.create(x, y)

Create a point2 object: { x, y }.

Parameters:

• x
  • a number. The x coordinate.
• y
  • a number. The y coordinate.

Returns:

• a point2

Source: create.js

affineplane.point2.delta

Alias of affineplane.point2.difference

affineplane.point2.diff

Alias of affineplane.point2.difference

affineplane.point2.difference(p, q)

A vector from point p to point q.

Parameters:

• p
  • a point2
• q
  • a point2

Returns:

• a vec2

Aliases: affineplane.point2.diff, affineplane.point2.delta, affineplane.point2.vectorTo

Source: difference.js

affineplane.point2.direction(p, q)

Get direction from point to point.

Parameters:

• p
  • a point2, the direction origin
• q
  • a point2, the direction target

Returns:

• a dir2, a unit vector. If no direction can be computed, for example in the case where the points are equal, then the direction will be { x: 1, y: 0 }

Source: direction.js

affineplane.point2.distance(p, q)

Distance between two points.

Parameters:

• p
  • a point2
• q
  • a point2

Returns:

• a number, a distance from p to q (= distance from q to p)

Source: distance.js

affineplane.point2.equal(p, q)

Test if points p, q are equal.

Parameters:

• p
  • a point2
• q
  • a point2

Returns:

• a boolean

Aliases: affineplane.point2.equals

Source: equal.js

affineplane.point2.equals

Alias of affineplane.point2.equal

affineplane.point2.fromArray(arrp)

Create { x, y } point from array [x, y].

Parameters:

• arrp
  • a two-element array

Returns:

• a point2

Source: fromArray.js

affineplane.point2.homothety(point, origin, ratio)

Perform homothety about the origin point.

Parameters:

• point
  • a point2
• origin
  • a point2, the pivot point
• ratio
  • a number, the scaling ratio

Returns:

• a point2

Source: homothety.js

affineplane.point2.mean

Alias of affineplane.point2.average

affineplane.point2.move

Alias of affineplane.point2.translate

affineplane.point2.offset(p, dx, dy)

Offset a point by scalars dx dy.

Parameters:

• p
  • a point2
• dx
  • a number, an offset along x-axis.
• dy
  • a number, an offset along y-axis.

Returns:

• a point2, translated by the vector { x: dx, y: dy }

Source: offset.js

affineplane.point2.polarOffset(p, distance, angle)

Create a point away from p at the given distance and angle.

Parameters:

• p
  • a point2
• distance
  • a number, the distance from p.
• angle
  • a number, the angle in radians

Returns:

• a point2

Source: polarOffset.js

affineplane.point2.projectByDistance(point, origin, distance)

Perform homothety about the origin point so that the point translates by the given distance. If the point and origin are the same point, no translation will occur and the original point is returned.

Parameters:

• point
  • a point2
• origin
  • a point2, the pivot point
• distance
  • a number, can be negative.

Returns:

• a point2

Source: projectByDistance.js

affineplane.point2.projectTo

Alias of affineplane.point2.projectToPlane

affineplane.point2.projectToLine(p, line)

Project a point orthogonally onto a line.

Parameters:

• p
  • a point2
• line
  • a line2

Returns:

• a point2

Source: projectToLine.js

affineplane.point2.projectToPlane(point, plane[, camera])

Project a point onto another plane in 3d. If camera is given, project perspectively. Otherwise, project orthogonally.

Parameters:

• point
  • a point2 in the reference space, assume z=0.
• plane
  • a plane3 in the reference space.
• camera
  • optional point3 in the reference space.

Returns:

• a point2 on the target plane.

Aliases: affineplane.point2.projectTo

Source: projectToPlane.js

affineplane.point2.rotateBy(p, origin, radians)

Rotate point about the given center.

Parameters:

• p
  • a point2
• origin
  • a point2, the point around to rotate
• radians
  • a number, angle in radians

Returns:

• a point2

Source: rotateBy.js

affineplane.point2.toArray(p)

Get the point2 object as an array.

Parameters:

• p
  • a point2

Returns:

• an array [x, y]

Source: toArray.js

affineplane.point2.transform(p, tr)

Transform a point.

Parameters:

• p
  • a point2
• tr
  • a helm2, a transform

Returns:

• a point2, the transformed point

Source: transform.js

affineplane.point2.transformMany(ps, tr)

Transform an array of points.

Parameters:

• ps
  • an array, of point2
• tr
  • a helm2, a transform

Returns:

• an array of point2, each point transformed by tr.

Source: transformMany.js

affineplane.point2.transitFrom(point, source)

Transit a point2 from the source plane to the reference plane.

Parameters:

• point
  • a point2 on the source plane.
• source
  • a plane2, the source plane, represented on the reference plane.

Returns:

• a point2, represented on the reference plane.

Source: transitFrom.js

affineplane.point2.transitTo(point, target)

Transit a point2 to a target plane. In other words, represent the point2 in the coordinate system of the plane.

Parameters:

• point
  • a point2 on the reference plane.
• target
  • a plane2, the target plane, represented on the reference plane.

Returns:

• a point2, represented on the target plane.

Source: transitTo.js

affineplane.point2.translate(p, vec)

Translate the point by the given vector. See affineplane.point2.offset to translate by scalars.

Parameters:

• p
  • a point2
• vec
  • a vec2

Returns:

• a point2

Aliases: affineplane.point2.move

Source: translate.js

affineplane.point2.validate(p)

Check if the object is a valid point2. Valid point2 has x and y properties that are valid numbers.

Parameters:

• p
  • an object

Returns:

• a boolean, true if valid point2

Source: validate.js

affineplane.point2.vectorTo

Alias of affineplane.point2.difference

affineplane.point3

Three-dimensional point { x, y, z }. Unlike vectors, points model locations in space and therefore are affected by scale, orientation, and translation of the plane on which they are represented.

Contents:

• affineplane.point3.ZERO
• affineplane.point3.almostEqual
• affineplane.point3.average
• affineplane.point3.copy
• affineplane.point3.create
• affineplane.point3.delta
• affineplane.point3.diff
• affineplane.point3.difference
• affineplane.point3.direction
• affineplane.point3.distance
• affineplane.point3.distanceToLine
• affineplane.point3.distanceToPlane
• affineplane.point3.distanceToRay
• affineplane.point3.equal
• affineplane.point3.equals
• affineplane.point3.fromArray
• affineplane.point3.homothety
• affineplane.point3.mean
• affineplane.point3.offset
• affineplane.point3.polarOffset
• affineplane.point3.projectByDistance
• affineplane.point3.projectTo
• affineplane.point3.projectToPlane
• affineplane.point3.rotateAroundLine
• affineplane.point3.rotateBy
• affineplane.point3.round
• affineplane.point3.toArray
• affineplane.point3.transitFrom
• affineplane.point3.transitTo
• affineplane.point3.translate
• affineplane.point3.translateBy
• affineplane.point3.validate
• affineplane.point3.vectorTo

Source: point3/index.js

affineplane.point3.ZERO

The zero point

Source: point3/index.js

affineplane.point3.almostEqual(p, q[, epsilon])

Test if points are almost equal by the margin of epsilon.

Parameters:

• p
  • a point3
• q
  • a point3
• epsilon
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.point3.average(ps)

Average of points.

Parameters:

• ps
  • array of point3

Returns:

• a point3

Aliases: affineplane.point3.mean

Source: average.js

affineplane.point3.copy(p)

Clone point3 to a new object.

Returns:

• a point3

Source: copy.js

affineplane.point3.create(x, y, z)

Create a three-dimensional point {x, y, z}.

Returns:

• a point3

Source: create.js

affineplane.point3.delta

Alias of affineplane.point3.difference

affineplane.point3.diff

Alias of affineplane.point3.difference

affineplane.point3.difference(p, q)

A vector from point p to point q.

Parameters:

• p
  • a point3
• q
  • a point3

Returns:

• a vec3

Aliases: affineplane.point3.diff, affineplane.point3.delta, affineplane.point3.vectorTo

Source: difference.js

affineplane.point3.direction(p, q)

Get direction from point to point.

Parameters:

• p
  • a point3, the direction origin
• q
  • a point3, the direction target

Returns:

• a dir3, a unit vector. If no direction can be computed, for example in the case where the points are equal, then the direction will be { x: 1, y: 0, z: 0 }

Source: direction.js

affineplane.point3.distance(p, q)

Euclidean distance between two points.

Parameters:

• p
  • a point3
• q
  • a point3

Returns:

• a number, a distance from p to q (= distance from q to p)

Source: distance.js

affineplane.point3.distanceToLine(p, line)

Compute the smallest euclidean distance between a point and a line. See also affineplane.point3.distanceToRay.

Parameters:

• p
  • a point3
• line
  • a line3

Returns:

• a number, a scalar1, a dist3, a distance

Source: distanceToLine.js

affineplane.point3.distanceToPlane(p, plane)

Euclidean distance between point and plane.

Parameters:

• p
  • a point3
• plane
  • a plane3

Returns:

• a number, a scalar1, a dist3, a distance

Source: distanceToPlane.js

affineplane.point3.distanceToRay(p, ray)

Compute the smallest euclidean distance between a point and a ray. For half of the space, the closest point on the ray is the ray origin and therefore, for points inside that half, the computation reduces to the euclidean distance to the ray origin. See also affineplane.point3.distanceToLine.

Parameters:

• p
  • a point3
• ray
  • a ray3

Returns:

• a number, a scalar1, a dist3, a distance

Source: distanceToRay.js

affineplane.point3.equal(p, q)

Test if points p, q are equal in value.

Parameters:

• p
  • a point3
• q
  • a point3

Returns:

• a boolean, true if equal

Aliases: affineplane.point3.equals

Source: equal.js

affineplane.point3.equals

Alias of affineplane.point3.equal

affineplane.point3.fromArray(arrp)

Create a point3 from array [x, y, z].

Parameters:

• arrp
  • a three-element array

Returns:

• a point3

Source: fromArray.js

affineplane.point3.homothety(point, origin, ratio)

Perform a homothety about the origin point.

Parameters:

• point
  • a point3
• origin
  • a point3
• ratio
  • a number

Returns:

• a point3

Source: homothety.js

affineplane.point3.mean

Alias of affineplane.point3.average

affineplane.point3.offset(p, dx, dy, dz)

Offset a point by scalars dx, dy, dz.

Parameters:

• p
  • a point3
• dx
  • a number, the offset along x-axis
• dy
  • a number, the offset along y-axis
• dz
  • a number, the offset along z-axis

Returns:

• a point3, translated by the vector { x: dx, y: dy, z: dz }

Source: offset.js

affineplane.point3.polarOffset(p, distance, roll, pitch)

Create a point near p at the given distance, roll angle, and pitch angle.

Parameters:

• p
  • a point3
• distance
  • a number, the distance from p.
• roll
  • a number, the roll angle in radians. Clockwise rotation, the right-hand rule for z-axis.
• pitch
  • optional number, default 0. The pitch angle in radians. The right-hand rule for x-axis.

Returns:

• a point3

Source: polarOffset.js

affineplane.point3.projectByDistance(point, origin, distance)

Perform homothety about the origin point so that the point translates by the given distance. If the point and origin are the same point, no translation will occur and the original point is returned.

Parameters:

• point
  • a point3
• origin
  • a point3, the pivot point
• distance
  • a number, can be negative.

Returns:

• a point3

Source: projectByDistance.js

affineplane.point3.projectTo

Alias of affineplane.point3.projectToPlane

affineplane.point3.projectToPlane(point, plane[, camera])

Project a 3D point onto a plane in 3D space.

Parameters:

• point
  • a point3 in the reference space.
• plane
  • a plane3 in the reference space. The target plane.
• camera
  • optional point3 in the reference space. The camera position.

Returns:

• a point2 on the target plane.

Aliases: affineplane.point3.projectTo

Source: projectToPlane.js

affineplane.point3.rotateAroundLine(p, line, rads)

Rotate a point around the axis line by the given radians.

Parameters:

• p
  • a point3
• line
  • a line3, the rotation axis
• rads
  • a number, angle in radians

Returns:

• a point3, the rotated point

Source: rotateAroundLine.js

affineplane.point3.rotateBy(p, origin, roll[, pitch])

Rotate point around the given center point. Roll is applied before pitch.

Parameters:

• p
  • a point3
• origin
  • a point3, the point around to rotate
• roll
  • a number, roll angle in radians. Right-hand rotation around z-axis.
• pitch
  • optional number, pitch angle in radians. Default 0. Right-hand rotation around x-axis.

Returns:

• a point3

Source: rotateBy.js

affineplane.point3.round(p)

Move point to the closest integer coordinate.

Parameters:

• p
  • a point3

Returns:

• a point3, having integer coordinates.

Source: round.js

affineplane.point3.toArray(p)

Get the point3 object as an array. Compatible with affineplane.point3.fromArray.

Parameters:

• p
  • a point3

Returns:

• an array [x, y, z]

Source: toArray.js

affineplane.point3.transitFrom(point, plane)

Represent the point on the reference plane without losing information.

Parameters:

• point
  • a point3 on the source plane.
• plane
  • a plane3 on the reference plane. The source plane.

Returns:

• a point3, represented on the reference plane.

Source: transitFrom.js

affineplane.point3.transitTo(point, plane)

Represent the point on the target plane without losing information.

Parameters:

• point
  • a point3 on the reference plane.
• plane
  • a plane3 on the reference plane. The target plane.

Returns:

• a point3, represented on the target plane.

Source: transitTo.js

affineplane.point3.translate(p, vec)

Translate the point by the given vector.

Parameters:

• p
  • a point3
• vec
  • a vec3 or vec2

Returns:

• a point3

Aliases: affineplane.point3.translateBy

Source: translate.js

affineplane.point3.translateBy

Alias of affineplane.point3.translate

affineplane.point3.validate(p)

Check if the object is a valid point3. Valid point3 has props x, y and z that are valid numbers.

Parameters:

• p
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.point3.vectorTo

Alias of affineplane.point3.difference

affineplane.poly2

A two-dimensional polygon; Array of point2; A closed sequence of points [{ x, y }, { x, y }, ...].

Contents:

• affineplane.poly2.create

Source: poly2/index.js

affineplane.poly2.create(points)

Create a polygon on plane. Deep-clones the points array.

Parameters:

• points
  • array of point2

Returns:

• a poly2, array of points

Source: create.js

affineplane.quat4

A quaternion { a, b, c, d }

Contents:

• affineplane.quat4.add
• affineplane.quat4.conjugate
• affineplane.quat4.create
• affineplane.quat4.diff
• affineplane.quat4.difference
• affineplane.quat4.fromDirectionAndAngle
• affineplane.quat4.fromVector
• affineplane.quat4.hamilton
• affineplane.quat4.multiply
• affineplane.quat4.norm
• affineplane.quat4.rotateVector

Source: quat4/index.js

affineplane.quat4.add(q, p)

Add two quaternions together via component-wise addition.

Parameters:

• q
  • a quat4
• p
  • a quat4

Returns:

• a quat4

Source: add.js

affineplane.quat4.conjugate(q)

Get the conjugate of a quaternion.

Parameters:

• q
  • a quat4

Returns:

• a quat4

Source: conjugate.js

affineplane.quat4.create(a, b, c, d)

Parameters:

• a
  • a number
• b
  • a number
• c
  • a number
• d
  • a number

Returns:

• a quat4

Source: create.js

affineplane.quat4.diff

Alias of affineplane.quat4.difference

affineplane.quat4.difference(q, p)

Get the quaternion q - p.

Parameters:

• q
  • a quat4
• p
  • a quat4

Returns:

• a quat4

Aliases: affineplane.quat4.diff

Source: difference.js

affineplane.quat4.fromDirectionAndAngle(dir, angle)

Construct a unit quaternion from an axis vector and a rotation angle around that direction. Note that if this quaternion is later used to rotate a 3D vector, the rotation angle will be applied twice to map the vector back to 3D.

Parameters:

• dir
  • a dir3 or a vec3
• angle
  • a number, an angle in radians

Returns:

• a quat4

Source: fromAxisAngle.js

affineplane.quat4.fromVector(vec)

Construct a vector quaternion i.e. a quaternion with zero scalar part.

Parameters:

• vec
  • a vec3

Returns:

• a quat4

Source: fromVector.js

affineplane.quat4.hamilton(q, p)

The Hamilton product of two quaternions.

Parameters:

• q
  • a quat4
• p
  • a quat4

Returns:

• a quat4

Aliases: affineplane.quat4.multiply

Source: hamilton.js

affineplane.quat4.multiply

Alias of affineplane.quat4.hamilton

affineplane.quat4.norm(q)

The length of quaternion. Also called the norm.

Parameters:

• q
  • a quat4

Returns:

• a number

Source: norm.js

affineplane.quat4.rotateVector(quat, vec)

Apply quaternion to rotate a vector. Note that the quaternion must rotate the vector twice to return it back to the 3D space. Therefore, if the quaternion was created using an angle like π/2, the vector will be rotated twice that amount, π.

Parameters:

• quat
  • a quat4, a quaternion.
• vec
  • a vec3, the vector to rotate

Returns:

• a vec3, the rotated vector.

Source: rotateVector.js

affineplane.ray3

Ray is like a line but extends into one direction only from the origin.

We represent ray with object { x, y, z, dx, dy, dz }

Contents:

• affineplane.ray3.DEFAULT
• affineplane.ray3.ZERO
• affineplane.ray3.almostEqual
• affineplane.ray3.at
• affineplane.ray3.copy
• affineplane.ray3.create
• affineplane.ray3.getOrigin
• affineplane.ray3.getVector
• affineplane.ray3.homothety
• affineplane.ray3.invert
• affineplane.ray3.negate
• affineplane.ray3.offset
• affineplane.ray3.transitFrom
• affineplane.ray3.transitTo
• affineplane.ray3.validate

Source: ray3/index.js

affineplane.ray3.DEFAULT

Default ray that has origin at zero and unit span along positive x-axis.

Source: ray3/index.js

affineplane.ray3.ZERO

Invalid ray with origin at zero and zero spanning vector.

Source: ray3/index.js

affineplane.ray3.almostEqual(r, rr[, epsilon])

Test if rays are almost equal by the margin of epsilon.

Parameters:

• r
  • a ray3
• rr
  • a ray3
• epsilon
  • Optional number, default to affineplane.epsilon.
  • Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.ray3.at(line, c)

Get a point on the ray at position c from the ray origin. For example, c=2 gives a point two ray spans away from the origin. Negative positions default to the ray origin.

Parameters:

• ray
  • a ray3
• c
  • a number

Returns:

• a point3

Source: at.js

affineplane.ray3.copy(r)

Copy ray object.

Parameters:

• r
  • a ray3

Returns:

• a ray3

Source: copy.js

affineplane.ray3.create(origin, span)

Create a ray object from origin point and a spanning vector.

Parameters:

• origin
  • a point3, the ray starting point.
• span
  • a dir3 or vec3, the ray direction and unit length along the ray.

Returns:

• a ray3

Source: create.js

affineplane.ray3.getOrigin(r)

Get the origin point of the ray. Note that you can also use the ray object itself as a point.

Parameters:

• r
  • a ray3

Returns:

• a point3

Source: getOrigin.js

affineplane.ray3.getVector(r)

Get the spanning vector of the ray.

Parameters:

• r
  • a ray3

Returns:

• a vec3

Source: getVector.js

affineplane.ray3.homothety(ray, origin, ratio)

Perform a homothety about the origin for the ray.

Parameters:

• ray
  • a ray3
• origin
  • a point3
• ratio
  • a number, the scaling ratio

Returns:

• a ray3

Source: homothety.js

affineplane.ray3.invert(r)

Get a ray with the same magnitude but to opposite direction.

Parameters:

• r
  • a ray3

Returns:

• a ray3

Aliases: affineplane.ray3.negate

Source: invert.js

affineplane.ray3.negate

Alias of affineplane.ray3.invert

affineplane.ray3.offset(ray, dx, dy, dz)

Offset a ray origin by scalars dx, dy, dz.

Parameters:

• ray
  • a ray3
• dx
  • a number, the offset along x-axis
• dy
  • a number, the offset along y-axis
• dz
  • a number, the offset along z-axis

Returns:

• a ray3

Source: offset.js

affineplane.ray3.transitFrom(ray, basis)

Represent the ray in the reference basis without losing information.

Parameters:

• ray
  • a ray3, represented in the given basis.
• basis
  • a plane3, represented in the reference basis.

Returns:

• a ray3, represented in the reference basis.

Source: transitFrom.js

affineplane.ray3.transitTo(ray, basis)

Represent the ray in another basis without losing information.

Parameters:

• ray
  • a ray3, represented in the reference basis.
• basis
  • a plane3, represented in the reference basis.

Returns:

• a ray3, represented in the given basis.

Source: transitTo.js

affineplane.ray3.validate(r)

Check if object is a valid ray3. Valid ray has numeric properties x, y, z, dx, dy, dz and has non-zero spanning vector.

Parameters:

• r
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.rect2

DEPRECATED in v2.10. Will be removed in v3.0. Use box2 instead.

Rectangle on a two-dimensional plane. A rectangle is an object { basis: { a, b, x, y }, size: { w, h } }, where the basis is a transformation from rectangle’s inner coordinate system to the reference coordinate system.

Contents:

• affineplane.rect2.at
• affineplane.rect2.atNorm
• affineplane.rect2.getArea
• affineplane.rect2.getArea
• affineplane.rect2.getBounds
• affineplane.rect2.getBounds
• affineplane.rect2.transitFrom
• affineplane.rect2.transitTo

Source: rect2/index.js

affineplane.rect2.at(rect, rx, ry)

Take a point on the rect, represented on the rects outer basis.

Parameters:

• rect
  • a rect2
• rx
  • horizontal distance from the top-left corner of the rectangle represented on the rects inner basis
• ry
  • vertical distance from the top-left corner of the rectangle represented on the rects inner basis

Returns:

• a point2 on the outer basis

Source: at.js

affineplane.rect2.atNorm(rect, nw, nh)

Take a point on the rect.

Parameters:

• rect
  • a rectangle
• nw
  • a number, a normalized coordinate along width 0..1
• nh
  • a number, a normalized coordinate along height 0..1

Returns:

• a point on the rectangle’s outer basis

Source: atNorm.js

affineplane.rect2.getArea(rect)

Compute rectangle area. This returns the area on the reference basis.

Parameters:

• rect
  • a rect2, on the reference basis.

Returns:

• a number, the area on the reference basis.

Source: getArea.js

affineplane.rect2.getArea(rect)

Compute rectangle area. This returns the area on the reference basis.

Parameters:

• rect
  • a rect2, on the reference basis.

Returns:

• a number, the area on the reference basis.

Source: getArea.js

affineplane.rect2.getBounds(rect)

Get outer bounds of the given rect. In other words, return a rectangle with no rotation and no dilation with respect to the reference basis but has translation and size so that it covers the given rectangle.

Parameters:

• rect
  • a rect2, on the reference basis.

Returns:

• a rect2, on the reference basis.

Source: getBounds.js

affineplane.rect2.getBounds(rect)

Get outer bounds of the given rect. In other words, return a rectangle with no rotation and no dilation with respect to the reference basis but has translation and size so that it covers the given rectangle.

Parameters:

• rect
  • a rect2, on the reference basis.

Returns:

• a rect2, on the reference basis.

Source: getBounds.js

affineplane.rect2.transitFrom(rect, source)

Convert a rectangle from source basis to the reference basis.

Parameters:

• rect
  • a rect2, a rectangle on the source basis.
• source
  • a plane2, the source basis represented on the reference basis.

Returns:

• a rect2, represented on the reference basis.

Source: transitFrom.js

affineplane.rect2.transitTo(rect, target)

Convert a rectangle from the reference basis to the target basis.

Parameters:

• rect
  • a rectangle on the reference basis.
• target
  • a plane2, the target basis represented on the reference basis.

Returns:

• a rect2, represented on the target basis.

Source: transitTo.js

affineplane.rect3

DEPRECATED in v2.10. Will be removed in v3.0. Use box3 instead.

A rectangle, floating in three dimensions. A rect3 is an object { basis: { a, b, x, y, z }, size: { w, h } }, where the basis is a helm3 - a Helmert transformation from rectangle’s inner coordinate system to the reference coordinate system.

Contents:

• affineplane.rect3.at
• affineplane.rect3.atNorm
• affineplane.rect3.create
• affineplane.rect3.transitFrom
• affineplane.rect3.transitTo

Source: rect3/index.js

affineplane.rect3.at(rect, rx, ry)

Take a point on the rect, represented on the rects outer basis.

Parameters:

• rect
  • a rect2
• rx
  • horizontal distance from the top-left corner of the rectangle represented on the rects inner basis
• ry
  • vertical distance from the top-left corner of the rectangle represented on the rects inner basis

Returns:

• a point3, represented on the outer basis.

Source: at.js

affineplane.rect3.atNorm(rect, nw, nh)

Take a point on the rect.

Parameters:

• rect
  • a rectangle
• nw
  • a number, a normalized coordinate along width 0..1
• nh
  • a number, a normalized coordinate along height 0..1

Returns:

• a point3, in the rectangle’s outer basis

Source: atNorm.js

affineplane.rect3.create(basis, size)

Construct a rect3 object from basis and size.

Parameters:

• basis
  • a basis3
• size
  • a size2

Returns:

• a rect3

Source: create.js

affineplane.rect3.transitFrom(rect, source)

Convert a rectangle from source basis to the reference basis.

Parameters:

• rect
  • a rect3, a rectangle on the source basis.
• source
  • a basis3, the source basis represented on the reference basis.

Returns:

• a rect3, represented on the reference basis.

Source: transitFrom.js

affineplane.rect3.transitTo(rect, target)

Convert a rectangle from the reference basis to the target basis.

Parameters:

• rect
  • a rectangle on the reference basis.
• target
  • a basis3, the target basis represented on the reference basis.

Returns:

• a rect3, represented on the target basis.

Source: transitTo.js

affineplane.rot2

Rotation in 2D. Represented by object { a, b }.

Contents:

• affineplane.rot2.create
• affineplane.rot2.validate

Source: rot2/index.js

affineplane.rot2.create(a, b)

Parameters:

• a
  • a number
• b
  • a number

Returns:

• a rot2

Source: create.js

affineplane.rot2.validate(r)

Check if the object is a valid rot2. Valid object has properties a and b which represent valid rotation matrix.

Parameters:

• r
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.scalar1

The scalar is a directionless, one-dimensional number. Suitable for lengths and scales that undergo basis transitions. If transited between bases, only a change in the coordinate scale affects the number representation of the scalar. Rotation or translation of the basis does not affect the scalar nor the representation.

Contents:

• affineplane.scalar1.almostEqual
• affineplane.scalar1.create
• affineplane.scalar1.equal
• affineplane.scalar1.projectToPlane
• affineplane.scalar1.transitFrom
• affineplane.scalar1.transitTo
• affineplane.scalar1.validate

Source: scalar1/index.js

affineplane.scalar1.almostEqual(c, d[, tolerance])

Test if scalars c, d are almost equal within the margin of tolerance.

Parameters:

• c
  • a number, a scalar1
• d
  • a number, a scalar1
• tolerance
  • optional number, default is affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.scalar1.create(d)

Create a valid scalar. Basically it is just the number itself.

Parameters:

• d
  • a number

Returns:

• a number, the scalar.

Throws:

• if the argument is not a number or is NaN

Source: create.js

affineplane.scalar1.equal(c, d)

Test if scalars c, d are strictly equal.

Parameters:

• c
  • a number, a scalar1
• d
  • a number, a scalar1

Returns:

• a boolean

Source: equal.js

affineplane.scalar1.projectToPlane(scalar, plane[, camera])

Project a scalar (e.g. distance) onto another plane in 3d. If camera is given, project perspectively. Otherwise, project orthogonally.

Parameters:

• scalar
  • a scalar1 on the z=0 plane of the reference space.
• plane
  • a plane3 relative to the reference space.
• camera
  • optional point3 in the reference space.

Returns:

• a scalar1, projected on the target plane, and represented in the scale of the target.

Source: projectToPlane.js

affineplane.scalar1.transitFrom(scalar, source)

Transit a scalar from the source basis to the reference basis.

Parameters:

• scalar
  • a number, a scalar1 in the source basis.
• source
  • a plane2 or plane3, the source basis, represented in the reference basis.

Returns:

• a number, the same scalar1 but represented in the reference basis.

Source: transitFrom.js

affineplane.scalar1.transitTo(scalar, target)

Transit a scalar to another basis. In other words, represent the scalar in the coordinate system of the target.

Parameters:

• scalar
  • a number, a scalar1 in the reference basis.
• target
  • a plane2 or plane3, the target basis, represented in the reference basis.

Returns:

• a number, a scalar1 in the target basis.

Source: transitTo.js

affineplane.scalar1.validate(s)

Check if the argument is a valid scalar1. Valid scalar1 is a number and not NaN.

Parameters:

• s
  • a value

Returns:

• a boolean, true if valid scalar1

Source: validate.js

affineplane.scalar2

The scalar2 is a directionless measure of order 2. It is suitable for area measurements that undergo basis transitions.

For example, let us have 1x1 square on a basis of scale 1. Area of the square is 1 unit. If we transit the square to a basis of scale 2, the square dimensions half to 0.5x0.5 and the area becomes, not half, but one fourth.

For another example, consider a map in scale 1:100. On the map, an area of 1 squaremeter of ground is represented by 1 squarecentimeter of paper, thus 1:10000 of the original area.

Contents:

• affineplane.scalar2.almostEqual
• affineplane.scalar2.create
• affineplane.scalar2.equal
• affineplane.scalar2.projectToPlane
• affineplane.scalar2.transitFrom
• affineplane.scalar2.transitTo
• affineplane.scalar2.validate

Source: scalar2/index.js

affineplane.scalar2.almostEqual(c, d[, tolerance])

Test if the second order scalars c, d are almost equal within the margin of tolerance.

Parameters:

• c
  • a number, a scalar2
• d
  • a number, a scalar2
• tolerance
  • optional number, default is affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.scalar2.create(d)

Create a valid scalar. Basically it is just the number itself.

Parameters:

• d
  • a number

Returns:

• a number, the scalar.

Throws:

• if the argument is not a number or is NaN

Source: create.js

affineplane.scalar2.equal(c, d)

Test if scalars c, d are strictly equal.

Parameters:

• c
  • a number, a scalar2
• d
  • a number, a scalar2

Returns:

• a boolean

Source: equal.js

affineplane.scalar2.projectToPlane(scalar, plane[, camera])

Project a second-order scalar (e.g. area) onto another plane in 3D. If camera is given, project perspectively. Otherwise, project orthogonally.

Parameters:

• scalar
  • a scalar2 on the z=0 plane of the reference space.
• plane
  • a plane3 relative to the reference space.
• camera
  • optional point3 in the reference space.

Returns:

• a scalar2, projected on the target plane, and represented in the scale of the target.

Source: projectToPlane.js

affineplane.scalar2.transitFrom(scalar, source)

Transit an area measure from the source basis to the reference basis.

Parameters:

• scalar
  • a number, a scalar2 in the source basis.
• source
  • a plane2 or plane3, the source basis, represented in the reference basis.

Returns:

• a number, the same scalar2 but represented in the reference basis.

Source: transitFrom.js

affineplane.scalar2.transitTo(scalar, target)

Transit an area measurement to another basis. In other words, represent a second order scalar in the coordinate system of the target.

Parameters:

• scalar
  • a number, a scalar2 in the reference basis.
• target
  • a plane2 or plane3, the target basis, represented in the reference basis.

Returns:

• a number, a scalar2 in the target basis.

Source: transitTo.js

affineplane.scalar2.validate(s)

Check if the argument is a valid scalar2. Valid scalar2 is a number and not NaN.

Parameters:

• s
  • a value

Returns:

• a boolean, true if valid scalar2

Source: validate.js

affineplane.scalar3

The scalar3 is a directionless measure of order 3. It is suitable for volume measurements that undergo basis transitions.

For example, let us have 1x1x1 box in a basis of scale 1. The volume of the box is 1 unit. If we transit the box into a basis of scale 2, the box dimensions half to 0.5x0.5x0.5 and the volume becomes, not half, but one eight.

For another example, consider a miniature building in scale 1:100. In the miniature, the volume of 1 cubic meter is represented by 1 cubic centimeter, thus 1:1000000 of the original volume.

Contents:

• affineplane.scalar3.almostEqual
• affineplane.scalar3.create
• affineplane.scalar3.equal
• affineplane.scalar3.transitFrom
• affineplane.scalar3.transitTo
• affineplane.scalar3.validate

Source: scalar3/index.js

affineplane.scalar3.almostEqual(c, d[, tolerance])

Test if the third-order scalars c, d are almost equal within the margin of tolerance.

Parameters:

• c
  • a number, a scalar3
• d
  • a number, a scalar3
• tolerance
  • optional number, default is affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.scalar3.create(d)

Create a valid third-order scalar. Basically it is just the number itself.

Parameters:

• d
  • a number

Returns:

• a number, the scalar.

Throws:

• if the argument is not a number or is NaN

Source: create.js

affineplane.scalar3.equal(c, d)

Test if the third-order scalars c, d are strictly equal.

Parameters:

• c
  • a number, a scalar2
• d
  • a number, a scalar2

Returns:

• a boolean

Source: equal.js

affineplane.scalar3.transitFrom(scalar, source)

Transit a volume measure from the source basis to the reference basis.

Parameters:

• scalar
  • a number, a scalar3 in the source basis.
• source
  • a plane2 or plane3, the source basis, represented in the reference basis.

Returns:

• a number, the same scalar2 but represented in the reference basis.

Source: transitFrom.js

affineplane.scalar3.transitTo(scalar, target)

Transit a volume measurement to another basis. In other words, represent a third-order scalar in the coordinate system of the target.

Parameters:

• scalar
  • a number, a scalar3 in the reference basis.
• target
  • a plane2 or plane3, the target basis, represented in the reference basis.

Returns:

• a number, a scalar3 in the target basis.

Source: transitTo.js

affineplane.scalar3.validate(s)

Check if the argument is a valid scalar3. Valid scalar3 is a number and not NaN.

Parameters:

• s
  • a value

Returns:

• a boolean, true if valid scalar3

Source: validate.js

affineplane.segment2

Two-dimensional line segment. Represented by the segment start and end points in an array of length two.

Example: [{ x: 0, y: 0 }, { x: 1, y: 2 }]

Contents:

• affineplane.segment2.collide
• affineplane.segment2.create
• affineplane.segment2.transitFrom
• affineplane.segment2.transitTo
• affineplane.segment2.validate

Source: segment2/index.js

affineplane.segment2.collide(s0, s1)

Test if two segments collide.

Parameters:

• s0
  • a segment2
• s1
  • a segment2

Returns:

• a boolean, true if segments collide.

Source: collide.js

affineplane.segment2.create(p0, p1)

Create a segment from points.

Parameters:

• p0
  • a point2
• p1
  • a point2

Returns:

• a segment2, an array.

Source: create.js

affineplane.segment2.transitFrom(seg, source)

Represent a segment on the reference basis. In other words, transit the segment from the source basis to the reference basis.

Parameters:

• seg
  • a segment2, represented on the source basis.
• source
  • a plane2, the source basis, represented on the reference basis.

Returns:

• a segment2, represented on the reference basis.

Source: transitFrom.js

affineplane.segment2.transitTo(seg, target)

Represent a segment in the target basis. In other words, transit the segment from the reference basis to the target basis.

Parameters:

• seg
  • a segment2, represented on the reference basis.
• target
  • a plane2, the target basis, represented on the reference basis.

Returns:

• a segment2, represented in the target basis.

Source: transitTo.js

affineplane.segment2.validate(seg)

Check if the object is a valid segment2. A valid segment2 is an array of two valid point2 objects.

Parameters:

• seg
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.segment3

Three-dimensional line segment. Represented by the segment start and end points in an array of length two.

Example: [{ x: 0, y: 0, z: 0 }, { x: 1, y: 2, z: 3 }]

Contents:

• affineplane.segment3.create
• affineplane.segment3.toVector
• affineplane.segment3.transitFrom
• affineplane.segment3.transitTo
• affineplane.segment3.validate

Source: segment3/index.js

affineplane.segment3.create(p0, p1)

Create a segment from points.

Parameters:

• p0
  • a point3
• p1
  • a point3

Returns:

• a segment3, an array.

Source: create.js

affineplane.segment3.toVector(seg)

Convert segment to a vector from the first to the second segment point.

Parameters:

• seg
  • a segment3

Returns:

• a vec3

Source: toVector.js

affineplane.segment3.transitFrom(seg, source)

Represent a segment in the reference basis. In other words, transit the segment from the source basis to the reference basis.

Parameters:

• seg
  • a segment3, represented in the source basis.
• source
  • a plane3, the source basis, represented in the reference basis.

Returns:

• a segment3, represented in the reference basis.

Source: transitFrom.js

affineplane.segment3.transitTo(seg, target)

Represent a segment in the target basis. In other words, transit the segment from the reference basis to the target basis.

Parameters:

• seg
  • a segment3, represented in the reference basis.
• target
  • a plane3, the target basis, represented in the reference basis.

Returns:

• a segment3, represented in the target basis.

Source: transitTo.js

affineplane.segment3.validate(seg)

Check if the object is a valid segment3. A valid segment3 is an array of two valid point3 objects.

Parameters:

• seg
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.size2

Two-dimensional rectangular size, consisting of width and height.

Represented with an object { w, h }.

Contents:

• affineplane.size2.area
• affineplane.size2.atNorm
• affineplane.size2.create
• affineplane.size2.scaleBy
• affineplane.size2.transitFrom
• affineplane.size2.transitTo
• affineplane.size2.validate

Source: size2/index.js

affineplane.size2.area(sz)

Area. If your w and h are in px, this gives you the total number of pixels.

Parameters:

• sz
  • a size2

Returns:

• a number

Source: area.js

affineplane.size2.atNorm(sz, nw, nh)

Find a point on the area.

Parameters:

• sz
  • a size2
• nw
  • a normalized width in 0..1
• nh
  • a normalized height

Returns:

• a point2

Source: atNorm.js

affineplane.size2.create(width, height)

Create a size2 object.

Parameters:

• width
  • a number
• height
  • a number

Returns:

• a size2

Source: create.js

affineplane.size2.scaleBy(sz, multiplier)

Scale and preserve aspect ratio. Multiplies all dimensions uniformly.

Parameters:

• sz
  • a size2
• multiplier
  • a number

Returns:

• a size2

Source: scaleBy.js

affineplane.size2.transitFrom(size, source)

Transit a size from the source plane to the reference plane.

Parameters:

• size
  • a size2 on the source plane.
• source
  • a plane2, the source plane, represented on the reference plane.

Returns:

• a size2, represented on the reference plane.

Source: transitFrom.js

affineplane.size2.transitTo(size, target)

Transit a size2 to a target plane. In other words, represent the size in the coordinate system of the target plane.

Parameters:

• size
  • a size2 on the reference plane.
• target
  • a plane2, the target plane, represented on the reference plane.

Returns:

• a size2 on the target plane.

Source: transitTo.js

affineplane.size2.validate(s)

Check if the object is a valid size2. Valid size2 has properties w,h that are valid numbers.

Parameters:

• s
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.size3

Three-dimensional cuboid size, consisting of width, height, and depth.

Represented with an object { w, h, d }.

Contents:

• affineplane.size3.atNorm
• affineplane.size3.create
• affineplane.size3.scaleBy
• affineplane.size3.transitFrom
• affineplane.size3.transitTo
• affineplane.size3.validate
• affineplane.size3.volume

Source: size3/index.js

affineplane.size3.atNorm(sz, nw, nh, nd)

Find a point in the volume.

Parameters:

• sz
  • a size3
• nw
  • a normalized width in 0..1
• nh
  • a normalized height
• nd
  • a normalized depth

Returns:

• a point3

Source: atNorm.js

affineplane.size3.create(width, height, depth)

Create a size3 object.

Parameters:

• width
  • a number
• height
  • a number
• depth
  • a number

Returns:

• a size3

Source: create.js

affineplane.size3.scaleBy(sz, multiplier)

Scale and preserve aspect ratio. Multiplies all dimensions uniformly.

Parameters:

• sz
  • a size3
• multiplier
  • a number

Returns:

• a size3

Source: scaleBy.js

affineplane.size3.transitFrom(size, source)

Transit a size from the source basis to the reference basis.

Parameters:

• size
  • a size3 on the source basis.
• source
  • a plane3, the source basis, represented on the reference basis.

Returns:

• a size3, represented on the reference basis.

Source: transitFrom.js

affineplane.size3.transitTo(size, target)

Transit a size3 to a target basis. In other words, represent the size in the coordinate system of the target.

Parameters:

• size
  • a size3 on the reference basis.
• target
  • a plane3, the target basis, represented on the reference basis.

Returns:

• a size3 on the target basis.

Source: transitTo.js

affineplane.size3.validate(s)

Check if the object is a valid size3. Valid size3 has properties w,h,d that are valid numbers.

Parameters:

• s
  • an object

Returns:

• a boolean, true if valid

Source: validate.js

affineplane.size3.volume(sz)

Volume. If your w, h, and d are in pixels, this gives you the total number of voxels.

Parameters:

• sz
  • a size3

Returns:

• a number

Source: volume.js

affineplane.sphere2

Two dimensional sphere, a circle.

Represented with an object { x, y, r } for the origin and the radius.

Aliases: affineplane.circle2

Contents:

• affineplane.sphere2.UNIT
• affineplane.sphere2.ZERO
• affineplane.sphere2.almostEqual
• affineplane.sphere2.area
• affineplane.sphere2.atCenter
• affineplane.sphere2.boundingBox
• affineplane.sphere2.boundingCircle
• affineplane.sphere2.collide
• affineplane.sphere2.collisionArea
• affineplane.sphere2.copy
• affineplane.sphere2.create
• affineplane.sphere2.fromPoints
• affineplane.sphere2.gap
• affineplane.sphere2.hasPoint
• affineplane.sphere2.homothety
• affineplane.sphere2.offset
• affineplane.sphere2.polarOffset
• affineplane.sphere2.rotateBy
• affineplane.sphere2.scaleBy
• affineplane.sphere2.size
• affineplane.sphere2.tangentCircle
• affineplane.sphere2.tangentCircles
• affineplane.sphere2.transitFrom
• affineplane.sphere2.transitTo
• affineplane.sphere2.translate
• affineplane.sphere2.validate

Source: sphere2/index.js

affineplane.sphere2.UNIT

The unit circle, radius=1.

Source: sphere2/index.js

affineplane.sphere2.ZERO

A zero-radius circle.

Source: sphere2/index.js

affineplane.sphere2.almostEqual(c, d[, tolerance])

Test if two spheres are almost equal by the margin of tolerance.

Parameters:

• c
  • a sphere2
• d
  • a sphere2
• tolerance
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.sphere2.area(sp)

Get area of the sphere.

Parameters:

• a sphere2

Returns:

• a scalar2, a number

Source: area.js

affineplane.sphere2.atCenter(sp)

Get the center point of the sphere. Note that the sphere2 object itself can act as a point2 in many cases.

Parameters:

• a sphere2

Returns:

• a point2

Source: atCenter.js

affineplane.sphere2.boundingBox(sphere)

Get outer rectangular boundary of the given sphere.

Parameters:

• sphere
  • a sphere2, in the reference basis.

Returns:

• a box2, in the reference basis.

Source: boundingBox.js

affineplane.sphere2.boundingCircle(circles)

Find a circle that encloses all the given circles. The result is approximate but is quaranteed to contain the optimal bounding circle.

Parameters:

• circles
  • an array of circle2

Returns:

• a circle2

Source: boundingCircle.js

affineplane.sphere2.collide(c, cc)

Detect collision between two spheres.

Parameters:

• c
  • a sphere2
• cc
  • a sphere2

Returns:

• boolean, true if the spheres collide

Source: collide.js

affineplane.sphere2.collisionArea(c, cc)

Compute collision area between two spheres.

Parameters:

• c
  • a sphere2
• cc
  • a sphere2

Returns:

• a scalar2, number, the area.

Source: collisionArea.js

affineplane.sphere2.copy(p)

Copy a sphere object.

Parameters:

• p
  • a sphere2

Returns:

• a sphere2

Source: copy.js

affineplane.sphere2.create(x, y, r)

Create a sphere2 object.

Parameters:

• x
  • a number
• y
  • a number
• r
  • a number, the radius

Returns:

• a sphere2

Source: create.js

affineplane.sphere2.fromPoints(p, q)

Create a sphere2 from two points, the origin p and the circumference point q.

Parameters:

• p
  • a point2, at the circle center.
• q
  • a point2, on the circle circumference.

Returns:

• a sphere2

Source: fromPoints.js

affineplane.sphere2.gap(c, cc)

The gap distance between the two spheres is the closest distance between their surfaces. The gap is zero or negative when the spheres collide.

Parameters:

• c
  • a sphere2
• cc
  • a sphere2 or a point2

Returns:

• a scalar1, a number, the closest distance between the sphere surfaces.

Source: gap.js

affineplane.sphere2.hasPoint(c, point)

Detect collision between a sphere and a point.

Parameters:

• c
  • a sphere2
• point
  • a point2

Returns:

• boolean, true if the point is inside the sphere or at the surface.

Source: hasPoint.js

affineplane.sphere2.homothety(sphere, origin, ratio)

Perform homothety for the sphere about a pivot. In other words, scale the sphere by the given ratio, so that the pivot point stays fixed.

Parameters:

• sphere
  • a sphere2
• origin
  • a point2, the transform origin, the pivot point
• ratio
  • a number, the scaling ratio

Returns:

• a sphere2

Aliases: affineplane.sphere2.scaleBy

Source: homothety.js

affineplane.sphere2.offset(c, dx, dy)

Offset a sphere by scalars dx, dy. See affineplane.sphere2.translate to offset by a vector.

Parameters:

• c
  • a sphere2
• dx
  • a number, an offset along x-axis.
• dy
  • a number, an offset along y-axis.

Returns:

• a sphere2, translated

Source: offset.js

affineplane.sphere2.polarOffset(sphere, distance, theta)

Offset a sphere by the given distance towards the direction given by the theta angles.

Parameters:

• sphere
  • a sphere2
• distance
  • a number, the distance from p.
• theta
  • a number, the angle around z-axis, the azimuthal angle. Clockwise rotation, following the right-hand rule.

Returns:

• a sphere2

Source: polarOffset.js

affineplane.sphere2.rotateBy(sp, origin, radians)

Rotate a sphere about an origin point.

Parameters:

• sp
  • a sphere2
• origin
  • a point2, the point around to rotate
• radians
  • a number, angle in radians

Returns:

• a sphere2, the rotated sphere

Source: rotateBy.js

affineplane.sphere2.scaleBy

Alias of affineplane.sphere2.homothety

affineplane.sphere2.size(sphere)

Get the rectangular size of the circle.

Parameters:

• sphere
  • a sphere2 in the reference basis.

Returns:

• a size2 in the reference basis.

Source: size.js

affineplane.sphere2.tangentCircle(ca, cb, r, righthand)

Find a circle C that is left-hand tangent to the circles A and B. Use the fourth parameter to switch to right-hand tangent. Note the coordinate system: x-axis points right and y-axis points down.

If the gap between A and B is too large for C to be tangent to both then the resulting circle is tangent with A and as close to B as possible. Under the righthand flag, the preference is reversed.

Parameters:

• ca
  • a sphere2 {x,y,r}, the circle A.
• cb
  • a sphere2 {x,y,r}, the circle B.
• r
  • a number, a dist2, the radius of the circle C.
• righthand
  • a boolean, default false. Set true to find right-hand tangent circle.

Returns:

• a sphere2 {x,y,r}

See also sphere2.tangentCircles for efficient computation of both hands with just one function call.

Source: tangentCircle.js

affineplane.sphere2.tangentCircles(ca, cb, r)

Find circles of radius r that are externally tangent to the given circles A and B. Usually there are two such circles, one at the left-hand side and one at the right-hand side with respect to the vector from A to B. The function returns the two circles in this left-right order.

If the gap between A and B is too large for the circles to be tangent to both A and B then the function compromises and returns two circles: the first is tangent to A at the direction of B and the second is tangent to B at the direction of A.

If the gap between A and B just fits a circle of radius r, the function returns only one circle.

If the circles A and B are nested, the function compromises and returns only one circle that is externally tangent to the larger one so that the returned circle is still as close to the smaller one as possible.

Parameters:

• ca
  • a circle {x,y,r}, the circle A.
• cb
  • a circle {x,y,r}, the circle B.
• r
  • a number, the radius of the circles to find.

Returns:

• an array of sphere2. The array contains either one or two sphere2.

See also sphere2.tangentCircle if you only need either the left-hand or right-hand result.

Source: tangentCircles.js

affineplane.sphere2.transitFrom(sphere, source)

Transit a sphere2 from the source plane to the reference plane.

Parameters:

• sphere
  • a sphere2 on the source plane.
• source
  • a plane2, the source plane, represented on the reference plane.

Returns:

• a sphere2, represented on the reference plane.

Source: transitFrom.js

affineplane.sphere2.transitTo(sphere, target)

Transit a sphere2 to a target plane. In other words, represent the sphere in the coordinate system of the target plane.

Parameters:

• sphere
  • a sphere2 on the reference plane.
• target
  • a plane2, the target plane, represented on the reference plane.

Returns:

• a sphere2, represented on the target plane.

Source: transitTo.js

affineplane.sphere2.translate(c, vec)

Translate the circle by the vector. Does not affect radius. See affineplane.sphere2.offset to translate by scalars.

Parameters:

• c
  • a sphere2
• vec
  • a vec2

Returns:

• a sphere2

Source: translate.js

affineplane.sphere2.validate(p)

Check if the object is a valid sphere2. A valid sphere2 has x, y, r properties that are valid numbers.

Parameters:

• p
  • an object

Returns:

• a boolean, true if valid sphere2

Source: validate.js

affineplane.sphere3

Three dimensional sphere.

Represented with an object { x, y, z, r } for the origin and the radius.

Contents:

• affineplane.sphere3.UNIT
• affineplane.sphere3.ZERO
• affineplane.sphere3.almostEqual
• affineplane.sphere3.area
• affineplane.sphere3.atCenter
• affineplane.sphere3.boundingBox
• affineplane.sphere3.boundingSphere
• affineplane.sphere3.collide
• affineplane.sphere3.copy
• affineplane.sphere3.create
• affineplane.sphere3.fromPoints
• affineplane.sphere3.gap
• affineplane.sphere3.hasPoint
• affineplane.sphere3.homothety
• affineplane.sphere3.offset
• affineplane.sphere3.polarOffset
• affineplane.sphere3.projectTo
• affineplane.sphere3.projectToPlane
• affineplane.sphere3.rotateAroundLine
• affineplane.sphere3.rotateBy
• affineplane.sphere3.scaleBy
• affineplane.sphere3.size
• affineplane.sphere3.transitFrom
• affineplane.sphere3.transitTo
• affineplane.sphere3.translate
• affineplane.sphere3.validate
• affineplane.sphere3.volume

Source: sphere3/index.js

affineplane.sphere3.UNIT

The unit sphere, radius=1.

Source: sphere3/index.js

affineplane.sphere3.ZERO

A zero-radius sphere.

Source: sphere3/index.js

affineplane.sphere3.almostEqual(c, d[, tolerance])

Test if two spheres are almost equal by the margin of tolerance.

Parameters:

• c
  • a sphere3
• d
  • a sphere3
• tolerance
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.sphere3.area(sp)

Get surface area of the sphere.

Parameters:

• a sphere3

Returns:

• a scalar2, a number. The area.

Source: area.js

affineplane.sphere3.atCenter(sp)

Get the center point of the sphere. Note that the sphere3 object itself can act as a point3 in many cases.

Parameters:

• sp
  • a sphere3

Returns:

• a point3

Source: atCenter.js

affineplane.sphere3.boundingBox(sphere)

Get outer cuboid boundary of the given sphere.

Parameters:

• sphere
  • a sphere3, in the reference basis.

Returns:

• a box3, in the reference basis.

Source: boundingBox.js

affineplane.sphere3.boundingSphere(spheres)

Find a sphere that encloses all the given spheres. The result is approximate but is quaranteed to contain the optimal bounding sphere.

Parameters:

• spheres
  • an array of sphere3

Returns:

• a sphere3

Source: boundingSphere.js

affineplane.sphere3.collide(c, cc)

Detect collision between two spheres.

Parameters:

• c
  • a sphere3
• cc
  • a sphere3

Returns:

• boolean, true if the spheres collide

Source: collide.js

affineplane.sphere3.copy(p)

Copy a sphere object.

Parameters:

• p
  • a sphere3

Returns:

• a sphere3

Source: copy.js

affineplane.sphere3.create(x, y, z, r)

Create a sphere3 object.

Parameters:

• x
  • a number
• y
  • a number
• z
  • a number
• r
  • a number, the radius

Returns:

• a sphere3

Source: create.js

affineplane.sphere3.fromPoints(p, q)

Create a sphere3 from two points, the origin p and the circumference point q.

Parameters:

• p
  • a point3, at the circle center.
• q
  • a point3, on the circle circumference.

Returns:

• a sphere3

Source: fromPoints.js

affineplane.sphere3.gap(c, cc)

The gap distance between the two spheres is the closest distance between their surfaces. The gap is zero or negative when the spheres collide.

Parameters:

• c
  • a sphere3
• cc
  • a sphere3 or a point3

Returns:

• a scalar1, a number, the closest distance between the sphere surfaces.

Source: gap.js

affineplane.sphere3.hasPoint(c, point)

Detect collision between a sphere and a point.

Parameters:

• c
  • a sphere3
• point
  • a point2

Returns:

• boolean, true if the point is inside the sphere or at the surface.

Source: hasPoint.js

affineplane.sphere3.homothety(sphere, origin, ratio)

Perform homothety for the sphere about a pivot. In other words, scale the sphere by the given ratio, so that the pivot point stays fixed.

Parameters:

• sphere
  • a sphere3
• origin
  • a point3, the transform origin, the pivot point
• ratio
  • a number, the scaling ratio

Returns:

• a sphere3

Aliases: affineplane.sphere3.scaleBy

Source: homothety.js

affineplane.sphere3.offset(c, dx, dy[, dz])

Offset a sphere by scalars dx, dy, dz. See affineplane.sphere3.translate to offset by a vector.

Parameters:

• c
  • a sphere3
• dx
  • a number, an offset along x-axis.
• dy
  • a number, an offset along y-axis.
• dz
  • optional number. The offset along z-axis, default is 0.

Returns:

• a sphere3, translated

Source: offset.js

affineplane.sphere3.polarOffset(sphere, distance, theta[, phi])

Offset a sphere by the given distance towards the direction given by the spherical theta and phi angles.

Parameters:

• sphere
  • a sphere3
• distance
  • a number, the distance from p.
• theta
  • a number, the angle around z-axis, the azimuthal angle. Clockwise rotation, following the right-hand rule.
• phi
  • optional number, default π/2. The polar angle in radians measured from the positive z-axis.

Returns:

• a sphere3

Source: polarOffset.js

affineplane.sphere3.projectTo

Alias of affineplane.sphere3.projectToPlane

affineplane.sphere3.projectToPlane(sphere, plane[, camera])

Project a 3D sphere onto a plane in 3D space. The result is a 2D sphere. If the camera is undefined, project orthogonally.

Parameters:

• sphere
  • a sphere3 in the reference space.
• plane
  • a plane3 in the reference space. The target plane.
• camera
  • optional point3 in the reference space. The camera position.

Returns:

• a sphere2 on the target plane.

Aliases: affineplane.sphere3.projectTo

Source: projectToPlane.js

affineplane.sphere3.rotateAroundLine(sp, line, rads)

Rotate a sphere around the axis line by the given radians.

Parameters:

• sp
  • a sphere3
• line
  • a line3, the rotation axis
• rads
  • a number, angle in radians

Returns:

• a sphere3, the rotated sphere

Source: rotateAroundLine.js

affineplane.sphere3.rotateBy(sp, origin, radians)

Rotate a sphere about a line parallel to z-axis that goes through the origin point. The rotation direction follows the right hand rule about the positive z-axis.

Parameters:

• sp
  • a sphere3
• origin
  • a point3, the point that defines the line around which to rotate
• radians
  • a number, angle in radians

Returns:

• a sphere3, the rotated sphere

Source: rotateBy.js

affineplane.sphere3.scaleBy

Alias of affineplane.sphere3.homothety

affineplane.sphere3.size(sphere)

Get the cuboid size of the sphere.

Parameters:

• sphere
  • a sphere3 in the reference basis.

Returns:

• a size3 in the reference basis.

Source: size.js

affineplane.sphere3.transitFrom(sphere, source)

Transit a sphere3 from the source plane to the reference plane.

Parameters:

• sphere
  • a sphere3 on the source plane.
• source
  • a plane3, the source plane, represented on the reference plane.

Returns:

• a sphere3, represented on the reference plane.

Source: transitFrom.js

affineplane.sphere3.transitTo(sphere, target)

Transit a sphere3 to a target plane. In other words, represent the sphere in the coordinate system of the target plane.

Parameters:

• sphere
  • a sphere3 on the reference plane.
• target
  • a plane3, the target plane, represented on the reference plane.

Returns:

• a sphere3, represented on the target plane.

Source: transitTo.js

affineplane.sphere3.translate(c, vec)

Translate the sphere by the vector. Does not affect radius. See affineplane.sphere3.offset to translate by scalars.

Parameters:

• c
  • a sphere3
• vec
  • a vec3

Returns:

• a sphere3

Source: translate.js

affineplane.sphere3.validate(p)

Check if the object is a valid sphere3. A valid sphere3 has x, y, z, r properties that are valid numbers.

Parameters:

• p
  • an object

Returns:

• a boolean, true if valid sphere3

Source: validate.js

affineplane.sphere3.volume(sp)

Get volume of the sphere.

Parameters:

• a sphere3

Returns:

• a scalar3, a number. The volume.

Source: volume.js

affineplane.vec2

Vector is a two dimensional dynamic movent between points, also known as a displacement vector. See affineplane.point2 for position vectors.

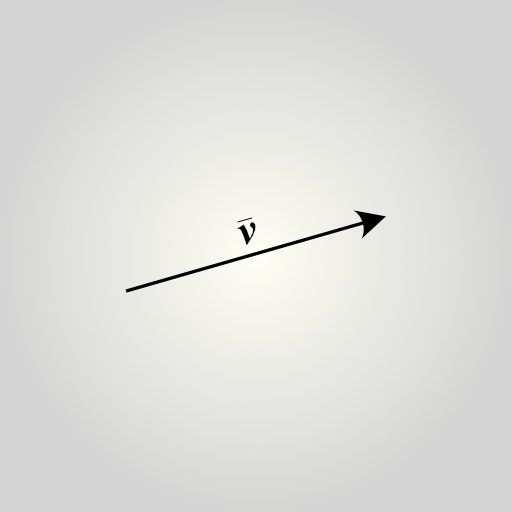
Contents:

• affineplane.vec2.ZERO
• affineplane.vec2.add
• affineplane.vec2.almostEqual
• affineplane.vec2.average
• affineplane.vec2.copy
• affineplane.vec2.create
• affineplane.vec2.cross
• affineplane.vec2.difference
• affineplane.vec2.divide
• affineplane.vec2.dot
• affineplane.vec2.equal
• affineplane.vec2.fromArray
• affineplane.vec2.fromPolar
• affineplane.vec2.independent
• affineplane.vec2.invert
• affineplane.vec2.magnitude
• affineplane.vec2.max
• affineplane.vec2.mean
• affineplane.vec2.min
• affineplane.vec2.negate
• affineplane.vec2.norm
• affineplane.vec2.normalize
• affineplane.vec2.projectTo
• affineplane.vec2.projectToPlane
• affineplane.vec2.projectToVector
• affineplane.vec2.rotateBy
• affineplane.vec2.rotateTo
• affineplane.vec2.scaleBy
• affineplane.vec2.scaleTo
• affineplane.vec2.sum
• affineplane.vec2.toArray
• affineplane.vec2.toPolar
• affineplane.vec2.transformBy
• affineplane.vec2.transitFrom
• affineplane.vec2.transitTo
• affineplane.vec2.unit
• affineplane.vec2.validate

Source: vec2/index.js

affineplane.vec2.ZERO

The zero vector in 2D

Source: vec2/index.js

affineplane.vec2.add(v, w)

Add two vectors. See vector.sum to add many vectors.

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a vec2

Source: add.js

affineplane.vec2.almostEqual(v, w[, epsilon])

Test if two vectors v and w are almost equal by the margin of epsilon.

Parameters:

• v
  • a vec2
• w
  • a vec2
• epsilon
  • optional number, default to affineplane.epsilon. Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.vec2.average(vs)

Arithmetic mean of an array of vectors.

Parameters:

• vs
  • an array of vec2

Returns:

• a vec2

Aliases: affineplane.vec2.mean

Source: average.js

affineplane.vec2.copy(v)

Copy vector object.

Parameters:

• v
  • a vec2

Returns:

• a vec2

Source: copy.js

affineplane.vec2.create(x, y)

Create a vector object { x, y }.

Parameters:

• x
  • a number. The translation along x-axis
• y
  • a number. The translation along y-axis

Returns:

• a vec2

Source: create.js

affineplane.vec2.cross(v, w)

The magnitude of cross product of two 2D vectors. While in 3D, the cross product returns a perpendicular vector, in 2D we must settle for a scalar result, the length of that 3D vector.

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a number

Source: cross.js

affineplane.vec2.difference(v, w)

A vector between v and w, in other words, v - w.

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a vec2

Source: difference.js

affineplane.vec2.divide(vec, divisor)

The division of a vector. Equivalent to multiplying the vector by the inverse of the divisor. The direction of the vector does not change.

Parameters:

• vec
  • a vec2
• divisor
  • a number

Returns:

• a vec2

Throws:

• if zero divisor

Source: divide.js

affineplane.vec2.dot(v, w)

The dot product of two vectors, also called the scalar product.

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a number

Source: dot.js

affineplane.vec2.equal(v, w)

Test if vectors v,w are equal

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a boolean

Source: equal.js

affineplane.vec2.fromArray(arrp)

Create { x, y } vector from array [x, y].

Parameters:

• arrp
  • an array

Returns:

• a vec2

Source: fromArray.js

affineplane.vec2.fromPolar(radius, direction)

Create a vector from polar coordinates.

Parameters:

• radius
  • a number, radial length from the origin
• direction
  • a number, angle in radians

Returns:

• a vec2

Source: fromPolar.js

affineplane.vec2.independent(v, w)

Test if the two vectors are linearly independent or almost so within the margin of affineplane.epsilon.

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a boolean, true if vectors are independent.

Source: independent.js

affineplane.vec2.invert(v)

Negate the vector. For example inverse({ x: 1, y: -1 }) returns { x: -1, y: 1 }.

Parameters:

• v
  • a vec2

Returns:

• a vec2

Aliases: affineplane.vec2.negate

Source: invert.js

affineplane.vec2.magnitude(v)

The length of the vector.

Parameters:

• v
  • a vec2

Returns:

• a number

Aliases: affineplane.vec2.norm

Source: magnitude.js

affineplane.vec2.max(v, w)

Element-wise maximum of two vectors.

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a vec2

Source: max.js

affineplane.vec2.mean(vs)

Alias of affineplane.vec2.average

affineplane.vec2.min(v, w)

Element-wise minimum of two vectors

Parameters:

• v
  • a vec2
• w
  • a vec2

Returns:

• a vec2

Source: min.js

affineplane.vec2.negate

Alias of affineplane.vec2.invert

affineplane.vec2.norm

Alias of affineplane.vec2.magnitude

affineplane.vec2.normalize

Alias of affineplane.vec2.unit

affineplane.vec2.projectTo

Alias of affineplane.vec2.projectToPlane

affineplane.vec2.projectToPlane(v, plane[, camera])

Project a vector onto another plane. If camera is given, project perspectively. Otherwise, project orthogonally.

Parameters:

• v
  • a vec2 in the reference space, z=0.
• plane
  • a plane3 in the reference space. The projection plane.
• camera
  • optional point3 in the reference space.

Returns:

• a vec2 on the projection plane.

Aliases: affineplane.vec2.projectTo

Source: projectToPlane.js

affineplane.vec2.projectToVector(v, w)

Project a vector onto the line specified by another vector. In other words, get the component of a vector that is parallel with another vector.

Parameters:

• v
  • a vec2 to be projected.
• w
  • a vec2, defines the line to project to.

Returns:

• a vec2, parallel with w.

Source: projectToVector.js

affineplane.vec2.rotateBy(v, radians)

Rotate vector by the given angle.

Parameters:

• v
  • a vec2
• radians
  • a number, from positive x-axis towards positive y-axis

Returns:

• a vec2

Source: rotateBy.js

affineplane.vec2.rotateTo(v, radians)

Rotate vector so that it points to the given angle.

Parameters:

• v
  • a vec2
• radians
  • a number from positive x-axis towards positive y-axis

Returns:

• a vec2

Source: rotateTo.js

affineplane.vec2.scaleBy(vec, multiplier)

The scalar multiplication of a vector. Scale the vector by a multiplier. The direction of the vector does not change.

Parameters:

• vec
  • a vec2
• multiplier
  • a number

Returns:

• a vec2

Source: scaleBy.js

affineplane.vec2.scaleTo(vec, magnitude)

Scale the vector to a certain length. The direction of the vector does not change. As an exception, zero vector length remains zero.

Parameters:

• vec
  • a vec2, non-zero vector.
• magnitude
  • a number, the target vector length.

Returns:

• a vec2

Source: scaleTo.js

affineplane.vec2.sum(vs)

Add an array of vectors together. See affineplane.vec2.add to add two vectors together.

Parameters:

• vs
  • an array of vec2. The array can be empty.

Returns:

• a vec2

Source: sum.js

affineplane.vec2.toArray(v)

Get the vector object as an array.

Parameters:

• v
  • a vec2

Returns:

• an array [x, y]

Source: toArray.js

affineplane.vec2.toPolar(v)

Get polar coordinates of a vector.

Parameters:

• v
  • a vec2

Returns:

• an object with properties:
  • radius
    • a number, the radial distance, the distance from z-axis.
  • magnitude
    • alias for radius. Will be removed in affineplane v3.
  • direction
    • a number, the azimuth angle in radians.

Source: toPolar.js

affineplane.vec2.transformBy(vec, tr)

Transform a vector. Translation does not affect the vector.

Parameters:

• vec
  • a vec2
• tr
  • a helm2

Returns:

• a vec2, the transformed vector

Source: transformBy.js

affineplane.vec2.transitFrom(vec, plane)

Transit a vec2 from the source plane to the reference plane. Translation of the plane does not affect the vector only scaling and rotation do.

Parameters:

• vec
  • a vec2 on the source plane.
• plane
  • a plane2, the source plane, represented on the reference plane.

Returns:

• a vec2, represented on the target plane.

Source: transitFrom.js

affineplane.vec2.transitTo(vec, plane)

Transit a vec2 to a target plane. In other words, represent the vec2 in the coordinate system of the plane. Translation of the plane does not affect the vector.

Parameters:

• vec
  • a vec2 on the reference plane.
• plane
  • a plane2, the target plane, represented on the reference plane.

Returns:

• a vec2, represented on the target plane.

Source: transitTo.js

affineplane.vec2.unit(v)

Get unit vector parallel to the given vector. The magnitude of unit vector is equal to one. If zero vector is given, assume direction towards positive x.

Parameters:

• v
  • a vec2

Returns:

• a vec2, magnitude of one.

Aliases: affineplane.vec2.normalize

Source: unit.js

affineplane.vec2.validate(v)

Check if object is a valid vec2.

Parameters:

• v
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.vec3

Three-dimensional vector, representing 3D movement of geometry. Vectors have no position in space, only direction and magnitude, and therefore their coordinates are affected only by plane scale and rotation when represented on different plane.

Contents:

• affineplane.vec3.ZERO
• affineplane.vec3.add
• affineplane.vec3.almostEqual
• affineplane.vec3.average
• affineplane.vec3.copy
• affineplane.vec3.create
• affineplane.vec3.cross
• affineplane.vec3.diff
• affineplane.vec3.difference
• affineplane.vec3.divide
• affineplane.vec3.dot
• affineplane.vec3.equal
• affineplane.vec3.fromArray
• affineplane.vec3.fromPolar
• affineplane.vec3.fromSpherical
• affineplane.vec3.independent
• affineplane.vec3.invert
• affineplane.vec3.magnitude
• affineplane.vec3.negate
• affineplane.vec3.norm
• affineplane.vec3.normalize
• affineplane.vec3.projectTo
• affineplane.vec3.projectToPlane
• affineplane.vec3.projectToVector
• affineplane.vec3.rotateAroundAxis
• affineplane.vec3.rotateBy
• affineplane.vec3.rotateBy
• affineplane.vec3.scaleBy
• affineplane.vec3.scaleTo
• affineplane.vec3.subtract
• affineplane.vec3.sum
• affineplane.vec3.toArray
• affineplane.vec3.toPolar
• affineplane.vec3.toSpherical
• affineplane.vec3.transformBy
• affineplane.vec3.transitFrom
• affineplane.vec3.transitTo
• affineplane.vec3.unit
• affineplane.vec3.validate

Source: vec3/index.js

affineplane.vec3.ZERO

The zero vector in 3D

Source: vec3/index.js

affineplane.vec4.ZERO

The zero vector in 4D

Source: vec4/index.js

affineplane.vec3.add(v, w)

Parameters:

• v
  • a vec3
• w
  • a vec3

Returns:

• a vec3

Source: add.js

affineplane.vec3.almostEqual(v, w[, epsilon])

Test if vectors are almost equal by the margin of epsilon.

Parameters:

• v
  • a vec3
• w
  • a vec3
• epsilon
  • Optional number, default to affineplane.epsilon.
  • Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.vec3.average(vs)

Arithmetic mean of an array of vectors.

Parameters:

• vs
  • array of vec3

Returns:

• a vec3

Source: average.js

affineplane.vec3.copy(v)

Clone the vector object.

Parameters:

• v
  • a vec3

Returns:

• a vec3

Source: copy.js

affineplane.vec3.create(x, y, z)

Parameters:

• x
  • a number
• y
  • a number
• z
  • a number

Returns:

• a vec3

Source: create.js

affineplane.vec3.cross(v, w)

The cross product of two 3D vectors. Returns a vector perpendicular to the given vectors. In other words, the result will be normal to the plane span by the given vectors.

Parameters:

• v
  • a vec3
• w
  • a vec3

Returns:

• a vec3

Source: cross.js

affineplane.vec3.diff(v, w)

Alias of affineplane.vec3.difference

affineplane.vec3.difference(v, w)

Get the vector v - w. In other words, if we place v, w to begin from the same point then the result is a vector from the end of w to the end of v.

Parameters:

• v
  • a vec3
• w
  • a vec3

Returns:

• a vec3

Aliases: affineplane.vec3.diff, affineplane.vec3.subtract

Source: difference.js

affineplane.vec3.divide(vec, divisor)

The division of a vector. Equivalent to multiplying the vector by the inverse of the divisor. The direction of the vector does not change.

Parameters:

• vec
  • a vec3
• divisor
  • a number. If zero, will result a vector having infinite length.

Returns:

• a vec3

Source: divide.js

affineplane.vec3.dot(v, w)

Dot product of two vectors, also called the scalar product.

Parameters:

• v
  • a vec3
• w
  • a vec3

Returns:

• a number

Source: dot.js

affineplane.vec3.equal(v, w)

Test if vectors v, w are equal in value.

Parameters:

• v
  • a vec3
• w
  • a vec3

Returns:

• a boolean, true if equal

Source: equal.js

affineplane.vec3.fromArray(arrv)

Create a vec3 from an array [x, y, z].

Parameters:

• arrv
  • an array

Returns:

• a vec3

Throws:

• if arrv has less than three elements.

Source: fromArray.js

affineplane.vec3.fromPolar(radius, direction, depth)

Create a vector from cylindrical polar coordinates. See also affineplane.vec3.toPolar.

Parameters:

• radius
  • a number, the radial distance from z-axis.
• direction
  • a number, the azimuth angle in radians.
• depth
  • optional number, default 0. The z coordinate.

Returns:

• a vec3

Source: fromPolar.js

affineplane.vec3.fromSpherical(magnitude, roll, pitch)

Create a vector from spherical polar coordinates. See also affineplane.vec3.toSpherical.

Parameters:

• magnitude
  • a number, the length of the vector.
• roll
  • a number, the roll angle in radians.
• pitch
  • optional number, default 0. The pitch angle in radians.

Returns:

• a vec3

Source: fromSpherical.js

affineplane.vec3.independent(v, w)

Test if the two vectors are linearly independent or almost so within the margin of affineplane.epsilon.

Parameters:

• v
  • a vec3
• w
  • a vec3

Returns:

• a boolean, true if vectors are independent.

Source: independent.js

affineplane.vec3.invert(v)

Get the vector -v.

Parameters:

• v
  • a vec3

Returns:

• a vec3

Aliases: affineplane.vec3.negate

Source: invert.js

affineplane.vec3.magnitude(v)

The euclidean length of the vector.

Parameters:

• v
  • a vec3

Returns:

• a number

Aliases: affineplane.vec3.norm

Source: magnitude.js

affineplane.vec3.negate

Alias of affineplane.vec3.invert

affineplane.vec3.norm

Alias of affineplane.vec3.magnitude

affineplane.vec3.normalize

Alias of affineplane.vec3.unit

affineplane.vec3.projectTo

Alias of affineplane.vec3.projectToPlane

affineplane.vec3.projectToPlane(vec, plane[, position, camera])

Project a 3D vector onto a 2D plane orthogonally. If a vector position and a camera positions are given, project the vector perspectively. Think of the vector as a displacement that acts at the given position. The resulting 2D vector is the component of that displacement parallel with the plane which would produce visually same movement.

Parameters:

• vec
  • a vec3, in the reference basis.
• plane
  • a plane3, in the reference basis. The image plane to which to project.
• position
  • optional point3, the vector position in the reference basis. The vector itself has only direction and magnitude, no position, and the perspective projection requires a position. If left undefined, will project orthogonally.
• camera
  • optional point3, the camera position in the reference basis. If left undefined, will project orthogonally.

Returns:

• a vec2 on the image plane.

Aliases: affineplane.vec3.projectTo

Source: projectToPlane.js

affineplane.vec3.projectToVector(v, w)

Project a vector onto the line specified by another vector. In other words, get the component of a vector that is parallel with another vector.

Parameters:

• v
  • a vec3 to be projected.
• w
  • a vec3, defines the line to project to.

Returns:

• a vec3, parallel with w.

Source: projectToVector.js

affineplane.vec3.rotateAroundAxis(v, axis, angle)

Rotate a vector by the given radian angle around the specified axis vector. The method uses Rodriques’ rotation formula under the hood. If you need to rotate multiple vectors simultaneously, it is probably better to construct a rotation matrix first and apply it to each vector.

Parameters:

• v
  • a vec3
• axis
  • a vec3, must not be a zero vector
• angle
  • a number, an angle in radians. Rotation around the axis. Rotation direction follows the right-hand rule.

Returns:

• a vec3

Source: rotateAroundAxis.js

affineplane.vec3.rotateBy(v, roll[, pitch])

Rotate vector by the given radian angles. Roll is applied before pitch.

Parameters:

• v
  • a vec3
• roll
  • a number, roll angle in radians. Right-hand rotation around z-axis.
• pitch
  • optional number, pitch angle in radians. Default 0. Right-hand rotation around x-axis.

Returns:

• a vec3

Source: rotateBy.js

affineplane.vec3.rotateBy(v, roll[, pitch])

Rotate vector so that it points to the given radian angles. The vector magnitude is preserved. Roll is applied before pitch.

Parameters:

• v
  • a vec3
• roll
  • a number, roll angle in radians. Right-hand rotation around z-axis.
• pitch
  • optional number, pitch angle in radians. Default 0. Right-hand rotation around x-axis.

Returns:

• a vec3

Source: rotateTo.js

affineplane.vec3.scaleBy(vec, multiplier)

The scalar multiplication of a vector. Scale the vector by a multiplier. The direction of the vector does not change.

Parameters:

• vec
  • a vec3
• multiplier
  • a number

Returns:

• a vec3

Source: scaleBy.js

affineplane.vec3.scaleTo(vec, magnitude)

Scale the vector to a certain length. The direction of the vector does not change. As an exception, zero vector length remains zero.

Parameters:

• vec
  • a vec3, non-zero vector.
• magnitude
  • a number, the target vector length

Returns:

• a vec3

Source: scaleTo.js

affineplane.vec3.subtract

Alias of affineplane.vec3.difference

affineplane.vec3.sum(vs)

Add an array of vectors together. See affineplane.vec3.add to add two vectors together.

Parameters:

• vs
  • an array of vec3. The array can be empty.

Returns:

• a vec3. If the array is empty, returns the zero vector.

Source: sum.js

affineplane.vec3.toArray(v)

Convert vector to array with elements [x, y, z].

Parameters:

• v
  • a vec3

Returns:

• an array

Source: toArray.js

affineplane.vec3.toPolar(v)

Get cylindrical polar coordinates of a vector.

Parameters:

• v
  • a vec3

Returns:

• object with properties
  • radius
    • a number, the radial distance, the distance from z-axis.
  • direction
    • a number, the azimuth angle in radians.
  • depth
    • a number, the z coordinate, the axial position.
  • magnitude
    • alias for radius, will be removed in affineplane v3

Source: toPolar.js

affineplane.vec3.toSpherical(v)

Get spherical polar coordinates for a vector. See also affineplane.vec3.fromSpherical.

Parameters:

• v
  • a vec3

Returns:

• object with properties:
  • magnitude
    • a number, the length of the vector.
  • roll
    • a number, the roll angle in radians.
  • pitch
    • a number, the pitch angle in radians.

Source: toSpherical.js

affineplane.vec3.transformBy(vec, tr)

Transform a vector. Translation does not affect the vector.

Parameters:

• vec
  • a vec3
• tr
  • a helm3

Returns:

• a vec3, the transformed vector

Source: transformBy.js

affineplane.vec3.transitFrom(vec, plane)

Represent the vector on the reference plane without losing information. Note that plane translation does not affect vectors.

Parameters:

• vec
  • a vec3 on the source plane.
• plane
  • a plane3 on the reference plane. The source plane.

Returns:

• a vec3, represented on the reference plane.

Source: transitFrom.js

affineplane.vec3.transitTo(vec, plane)

Represent the vec on the target plane without losing information.

Parameters:

• vec
  • a vec3 on the reference plane.
• plane
  • a plane3 on the reference plane. The target plane.

Returns:

• a vec3, represented on the target plane.

Source: transitTo.js

affineplane.vec3.unit(v)

Get unit vector parallel to the given vector. The magnitude of unit vector is equal to one. If zero vector is given, assume direction towards positive x.

Parameters:

• v
  • a vec3

Returns:

• a vec3, magnitude of one.

Aliases: affineplane.vec3.normalize

Source: unit.js

affineplane.vec3.validate(v)

Check if object is a valid vec3.

Parameters:

• v
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.vec4

A vec4 is a 4D vector { x, y, z, w }.

Contents:

• affineplane.vec4.ZERO
• affineplane.vec4.add
• affineplane.vec4.almostEqual
• affineplane.vec4.create
• affineplane.vec4.norm
• affineplane.vec4.scaleBy
• affineplane.vec4.validate

Source: vec4/index.js

affineplane.vec4.add(v, w)

Add two vectors together via component-wise addition.

Parameters:

• v
  • a vec4
• w
  • a vec4

Returns:

• a vec4

Source: add.js

affineplane.vec4.almostEqual(v, w[, epsilon])

Test if vectors are almost equal by the margin of epsilon.

Parameters:

• v
  • a vec4
• w
  • a vec4
• epsilon
  • Optional number, default to affineplane.epsilon.
  • Set to 0 for strict comparison.

Returns:

• a boolean

Source: almostEqual.js

affineplane.vec4.create(x, y, z, w)

Parameters:

• x
  • a number
• y
  • a number
• z
  • a number
• w
  • a number

Returns:

• a vec4

Source: create.js

affineplane.vec4.norm(v)

The length of 4D vector. Also called the norm.

Parameters:

• v
  • a vec4

Returns:

• a number

Source: norm.js

affineplane.vec4.scaleBy(v, m)

Scalar multiplication of a vector.

Parameters:

• v
  • a vec4
• m
  • a number, a multiplier

Returns:

• a vec4

Source: scaleBy.js

affineplane.vec4.validate(v)

Check if object is a valid vec4.

Parameters:

• v
  • an object

Returns:

• a boolean

Source: validate.js

affineplane.version

Package version string, for example '1.2.3'. We use semantic versioning.

↑ Back To Top

Source: lib/index.js

This site is open source. Improve this page.